1、单选题  152个球，放入若干个同样的箱子中，一个箱子最少放10个，最多放20个，且各个箱子的球数均不相同，问有多少种放法?(不计箱子的排列，即两种放法，经过箱子的重新排列后，是一样的，就算一种放法)_____
A: 1
B: 7
C: 12
D: 24
参考答案: A
本题解释:A【解析】 设箱子个数为m，因为每只箱子的球数均不相同，最少放10个，最多放20个，所以m≤20-10+1=11。如果m=11，那么球的总数≥10×11+（0+1+2+…+10）=110+55>152，所以m≤10。如果m≤9，那么球的总数≤10×9+（10+9+8+…+2）=90+54=144<152，所以m=10在m=10时，10×10+（10+9+…+1）=155=152+3，所以一个箱子放10个球，其余箱子分别放11，12，14，15，16，17，18，19，20个球，总数恰好为152，而且符合要求的放法也只有这一种。故本题正确答案为A。

2、单选题  如下图所示，AB两点是圆形体育场直径的两端，两人从AB点同时出发，沿环形跑道相向匀速而行，他们在距A点弧形距离80米处的C点第一次相遇，接着又在距B点弧形距离60米处的D点第二次相遇，问这个圆形体育场的周长是多少米?_____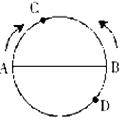A: 240
B: 300
C: 360
D: 420
参考答案: C
本题解释:正确答案是C考点行程问题解析解析1：根据题意可知两人第一个运动过程的路程和为半个圆周，第二个运动过程的路程和为整个圆周，因此每个人在两个过程中的路程比为1：2，设劣弧BC长为x，根据题意可得，80：(x+60)=1：2，解得x=100，因此圆周长为：2×(80+100)=360，故正确答案为C。解析2：此题为两次相遇问题，运用公式可得圆周长的一半为：80×3-60=180米，因此周长为360米，故正确答案为C。备注：两次相遇问题，两边型的两端点之间的距离公式：S=3A-B，其中S表示两端点之间的距离，A、B表示先后两次相遇点分别关于两个端点的距离。

3、单选题  某学校1999名学生去游故宫、景山和北海三地，规定每人至少去一处，至多去两地游览，那么至少有多少人游览的地方相同?_____
A: 35
B: 186
C: 247
D: 334
参考答案: D
本题解释:参考答案
题目详解:根据题意，可知：学生游玩一处的情况有3种，游玩2处的情况也有3种。学生游玩共有：3+3=6种情况，即共有6个抽屉。因为1999÷6=333…1，故至少有333+1=334人游览的地方相同考查点:数量关系>数学运算>抽屉原理问题>抽屉原理2

4、单选题  已知A: 2
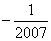B: C: 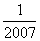D: 2008
参考答案: B
本题解释:参考答案:B
题目详解:根据题干可得：

5、单选题  海岛上信号站的值班员总用红、黄、白三色各三面旗向附近海域出示旗语，在旗杆上纵排挂，可以是一面、二面、三面。那么这样的旗语有多少种?_____
A: 21
B: 27
C: 33
D: 39
参考答案: D
本题解释:参考答案
题目详解:如果是一面旗：有3种旗语;如果是二面旗：有