1、单选题  某市为合理用电，鼓励各用户安装“峰谷”电表。该市原电价为每度0.53元，改装新电表后，每天晚上10点至次日早上8点为“低谷”，每度收取0.28元，其余时间为“高峰”，每度收取0.56元。为改装新电表每个用户须收取100元改装费。假定某用户每月用200度电，两个不同时段的耗电量各为100度。那么改装电表12个月后，该用户可节约_____元。
A: 161
B: 162
C: 163
D: 164
参考答案: D
本题解释:参考答案
题目详解:解法一：用户改装新表12个月共花费电费(0.28×100+0.56×100)×12=1008元，改装费100元，则：改装后所有花费为：1008+100=1108元;改装前所耗电费为：0.53×200×12=1272元;所以共节省：1272-1108=164元。解法二：根据题意，可知此题分为两个时间段。由于2个时间段都是100度，相当于每200度(一个周期)节约了：

2、单选题  为节约用水，某市决定用水收费实行超额超收，标准用水量以内每吨2.5元，超过标准的部分加倍收费。某用户某月用水15吨，交水费62.5元，若该用户下个月用水12吨，则应交水费多少钱?_____
A: 42.5元
B: 47.5元
C: 50元
D: 55元
参考答案: B
本题解释:参考答案:B
题目详解:如果该用户15吨水全部都交5元钱/吨，则他应当交75元水费，比实际缴纳额少了12.5元。少缴纳的12.5元是因为未超出标准用水量的部分，每吨缴纳2.5元，因此标准水量为：12.5÷2.5=5吨因此，无论是15吨或是12吨，都已经超过了标准水量，所以用水12吨时，应当比用水15吨少缴纳：3×5=15元因此，用水量为12吨时，应缴纳水费：62.5-15=47.5元。所以，选B。考查点:数量关系>数学运算>特殊情境问题>分段计算问题

3、单选题  某地收取电费的标准是：每月用电量不超过50度，每度收5角;如果超出50度，超出部分按每度8角收费。每月甲用户比乙用户多交3元3角电费，这个月甲、乙各用了多少度电?_____
A: 43,51
B: 51，43
C: 51，45
D: 45，51
参考答案: C
本题解释:参考答案:C
题目详解:观察题目，显然3元3角不能整除5角，所以甲一定超出了50度，而超出部分并不能整除8角，所以乙肯定没有超过50度。设甲比50度多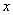

4、单选题  (2003国家，A类，第8题)某剧场共有100个座位，如果当票价为10元时，票能售完，当票价超过10元时，每升高2元，就会少卖出5张票。那么当总的售票收入为1360元时，票价为多少元?_____
A: 12元
B: 14元
C: 16元
D: 18元
参考答案: C
本题解释:参考答案:C
题目详解:解法一：根据票价和人数的关系，将选项代入，容易得到下表：

5、单选题  某城市居民用水价格为：每户每月不超过5吨的部分按4元/吨收取;超过5吨不超过10吨的部分按6元/吨收取;超过10吨的部分按8元/吨收取。某户居民两个月共交水费108元，则该户居民这两个月用水总量最多为多少吨?_____
A: 17.25
B: 21
C: 21.33
D: 24
参考答案: B
本题解释:参考答案:B
题目详解:解法一：在花费相同的情况下，要使两个月用水量最多，须使水价相对较便宜阶段的用水量最大即两个月的“不超过5吨”和“5吨到10吨”部分的水量尽量多，通过计算2×(4×5+6×5)=100元，剩余180-100=8元，由于超出10吨的部分按8元/吨收取，故用水量为2× 10+1=21吨，因此，选B。解法二：水量越大，费用越高，所以要用水最多，所以每个月应该用满10吨，所以总吨数为：