1、单选题  某公司中午订餐，周一有27人订餐，周二有39人订餐，周三有43人订餐，周四有41人订餐，周五有39人订餐。如果在这五天至少有一天订餐的人有39人，那么五天都订餐的最多有多少人?_____
A: 27
B: 26
C: 25
D: 24
参考答案: A
本题解释:参考答案:A
题目详解:依题意：将39人分为仅订餐一次和五天都订餐的;那么五天都订餐的最多有：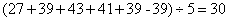

2、单选题  现有一个无限容积的空杯子，先加入1克酒精，再加入2克水，再加入3克酒精，再加入4克水，……，如此下去，问最终杯子中酒精溶液浓度为多少?_____
B: 25%
C: 33.3%
D: 50%
参考答案: D
本题解释:【解析】D。如果把加一次酒精和水看成一个流程，则经过n个流程后，杯子里面有1+3+5+…+(2n-1)=1/2n(1+2n-1)=n2克酒精，而酒精溶液有1+2+…+2n=1/2×2n(1+2n)=n(1+2n)克。故此时酒精溶液浓度为n2/n(1+2n)=n/(2n+1)，当n趋于无穷大时，溶液浓度趋于1/2=50%。思路点拨：极端法，当加入酒精或水的量极大时连续两次操作水与酒精的差距对整体的影响可以忽略不计，因此必然各占50%。

3、单选题  用2、3、4、5、6、7六个数字组成两个三位数，每个数字只用一次，这两个三位数的差最小是多少?_____
A: 47
B: 49
C: 69
D: 111
参考答案: A
本题解释:正确答案是A考点多位数问题解析因为每个数字只能用一次，显然首位决定大小，因此三个三位数的百位数字至少相差1，在这种情况下要使差值最小，则两个三位数为最接近，从而可知较小的三位数之末两位应尽可能大，而较大的三位数之末两位应尽可能小。在这个思想下，可知合适的三位数情况构造为523、476，此时三位数之末两位的差距最大，从而差值最小，最小差值为47。故正确答案为A。

4、单选题  某班有50名学生，在第一次测验中有26人得满分，在第二次测验中有21人得满分。如果两次测验中都没有得满分的学生有17人，那么两次测验中都获得满分的人数是多少?_____
A: 13
B: 14
C: 17
D: 20
参考答案: B
本题解释:正确答案是B考点容斥原理问题解析本题注意按照得满分得到两个类，进行容斥原理分析。设第一次测验得满分为事件A，第二次测验得满分为事件B，则两次都得满分为A∩B，将其设为x人，得过满分为A∪B。根据公式A∪B=A+B-A∩B可得：50-17=26+21-x解得x=14，因此两次测验中都获得满分的人数是14人，故正确答案为B。标签两集合容斥原理公式

5、单选题  小明和小红积极参加红领巾储蓄活动，把零用钱存入银行。小明存入银行的钱比小红少20元。如果两人都从银行取出12元买学习用品，那么小红剩下的钱是小明的3倍。问两人原来共存入银行多少元?_____
A: 44 
B: 64 
C: 75 
D: 86
参考答案: B
本题解释: B【解析】设小明存入银行x元，则小红存入银行（x+20）元。由题意可得：（x-12）×3=（x+20）-12，故x=22。所以两人原来共存入银行22+（22+20）=64（元）。