1、单选题  100人参加7项活动，已知每个人只参加一项活动，而且每项活动参加的人数都不一样，那么，参加人数第四多的活动最多有几个人参加?_____
A: 22
B: 21
C: 24
D: 23
参考答案: A
本题解释:正确答案是A考点多位数问题解析要保证“第四多的活动越多越好”，那么我们要求"其他活动的人越少越好“，其中有三个比其多，另外三个比其少，比”第四多“的少的最少的就是1、2、3，还剩下100-1-2-3=94，剩下四个活动需要尽量的接近，以保证”第四多“能够尽可能多，所以最好是四个连续的自然数，94÷4=23.5，所以这四个数分别为22、23、24、25，故正确答案为A。

2、单选题  一个快钟每小时比标准时间快3分钟，一个慢钟每小时比标准时间慢2分钟。如果将两个钟同时调到标准时间，结果在24小时内，快钟显示11点整时，慢钟显示9点半。则此时的标准时间是_____。
A: 10点35分
B: 10点10分
C: 10点15分
D: 10点06分
参考答案: D
本题解释:正确答案是D考点钟表问题解析应用比例，两个钟转动速度之差的比，即等于两钟钟面运行时长的差额之比。快钟与标准时间的之差、慢钟与标准时间的之差两者比为3：2，最终时间快钟、慢钟相差1.5小时，因此快钟与标准时间之差为1.5×3/5=0.9小时，则标准时间为11(时)-60×0.9(分)=10(时)06(分)。故正确答案为D。标签比例转化

3、单选题  有一种长方形小纸板，长为29毫米，宽为11毫米。现在用同样大小的这种小纸板拼合成一个正方形，问最少要多少块这样的小纸板_____
A: 197块
B: 192块
C: 319块
D: 299块
参考答案: C
本题解释:正确答案是C考点倍数约数问题解析本题可转化为求29与11的最小公倍数，即为29×11=319，则组成正方形的边长为319，从而可得组成正方形的小纸板数为319×319÷(29×11)=319(块)。故正确答案为C。

4、单选题  甲、乙两地相距210公里，a、b两辆汽车分别从甲、乙两地同时相向出发并连续往返于两地，从甲地出发的a汽车的速度为90公里/小时，从乙地出发的b汽车的速度为120公里/小时。问a汽车第二次从甲地出发后与b汽车相遇时，b汽车共行驶了多少公里?_____
A: 560公里
B: 600公里
C: 620公里
D: 630公里
参考答案: B
本题解释:正确答案是B考点行程问题解析a车第二次从甲出发前，经过一个往返的路程，即420公里，所用时间为420÷90=14/3小时;与此同时，b车经过路程为120×14/3=560公里，即一个往返路程加上140公里，此时ab两车位置如图所示。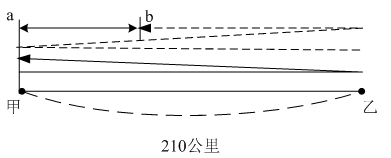

5、单选题  施工队要在一东西长600米的礼堂顶部沿东西方向安装一排吊灯，根据施工要求，必须在距西墙375米处安装一盏，并且各吊灯在东西墙之间均匀排列(墙角不能装灯)。该施工队至少需要安装多少盏吊灯?_____
A: 6
B: 7
C: 8
D: 9
参考答案: B
本题解释:正确答案是B考点计数模型问题解析本题考查植树问题。根据题意，可将顶部分为两段，一段为375，一段为225，因为吊灯要均匀排列，且求最小值，所以要求375和225的最大公约数，为75，即最大间隔为75;由于两端不植树，则可得600÷75+1-2=7(盏)。故正确答案为B。