1、单选题  甲、乙、丙三人，甲每分钟走50米，乙每分钟走40米，丙每分钟走35米，甲、乙从A地，丙从B地同时出发，相向而行，丙遇到甲2分钟后遇到乙，那么，A、B两地相距多少米?_____
A: 250米
B: 500米
C: 750米
D: 1275米
参考答案: D
本题解释:正确答案是D考点行程问题解析设AB两地相距s米，丙遇到乙的时间为t，则丙遇到甲的时间为(t+2)，由题意知s=(50+35)t，s=(40+35)(t+2)，解得s=1275，故正确答案为D。公式：相遇问题，相遇距离=(大速度+小速度)×相遇时间。秒杀技甲、乙从A地，丙从B地同时出发，相向而行，所以甲丙相对速度为50+35=85米/分钟，乙丙相对速度为40+35=75米/分钟，所以AB两地距离能整除85和75，只有D项1275符合要求，故正确答案为D。标签数字特性公式应用

2、单选题  某单位举办庆国庆茶话会，买来4箱同样重的苹果，从每箱取出24千克后，结果各箱所剩的苹果重量的和，恰好等于原来一箱的重量。那么原来每箱苹果重多少千克?_____
A: 16
B: 24
C: 32
D: 36
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析解析1：设原来每箱苹果重x千克，根据题意可得：4(x-24)=x，解得x=32，故选择C选项。解析2：原来一共4箱苹果，由“从每箱取出24千克后，结果各箱所剩的苹果重量的和，恰好等于原来一箱的重量”，可知总共取出来的苹果重量是原来3箱苹果的重量，因此原来每箱苹果的重量为：24×4÷3=32，故选择C选项。

3、单选题  将1～9个数字分别填入右边的九宫阵，使阵中每一行，每一列的三个数字之和均为15，其中的数字1可以填入阵中的_____位置。 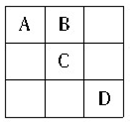A: A
B: B
C: C
D: D
参考答案: B
本题解释:正确答案是B考点趣味数学问题解析根据九宫格的性质，正中间的位置必填5，排除C;A与D为对称位置，本质上是一样，均可排除。故正确答案为B。

4、单选题  圆形的周长扩大至原来的2倍，它的面积比原来增大_____。
A: 1倍
B: 2倍
C: 3倍
D: 4倍
参考答案: C
本题解释:正确答案是C考点几何问题解析

5、单选题  铁路沿线的电线杆间隔是40米，某旅客在运行的火车中，从看到第一根电线杆到看到第51根电线杆正好是2分钟。这列火车每小时运行多少千米?_____
A: 50
B: 60
C: 70
D: 80
参考答案: B
本题解释:正确答案是B考点行程问题解析从第一根电线杆到第51根电线杆，火车经过的距离=(51-1)×40=2000(米)，2分钟行驶2000米，则火车每小时运行2000×(60/2)=60000(米)，即60千米，故正确答案为B。