1、单选题  有一盒乒乓球，每次8个8个的数，10个10个的数，12个12个的数，最后总是剩下3个。但是9个9个数，刚好数完，问这盒乒乓球至少有多少个?_____
A: 144
B: 180
C: 243
D: 324
参考答案: C
本题解释:参考答案:C
题目详解:每次8个8个的数，10个10个的数，12个12个的数，最后总是剩下3个，因此此题是余数问题中余同的情况。即根据"余同取余，最小公倍数做周期"可知：8、10、12的最小公倍数120，只需要用3加上最小公倍数，直至能够被9整除为止;容易得到，

2、单选题  学校举行运动会.要求按照红、黄、绿、紫的颜色插彩旗于校门口，请问第58面旗是什么颜色?_____
A: 黄
B: 红
C: 绿
D: 紫
参考答案: A
本题解释:参考答案:A
题目详解:依题意：按照红、黄、绿、紫排列;应用中国剩余定理：即

3、单选题  袋子里有一百多个小球，五个五个取出来剩余4个，六个六个取出来剩余3个，八个八个取出来剩余1个，问袋子里面有多少个小球?_____
A: 109
B: 119
C: 129
D: 139
参考答案: C
本题解释:参考答案:C
题目详解:设小球共有

4、单选题  一个数被3除余1，被4除余2，被5除余4，1000以内这样的数有多少个?_____
A: 15
B: 17
C: 18
D: 19
参考答案: B
本题解释:参考答案:B
题目详解:3、4的最小公倍数为12;根据"差同减差，公倍数做周期"可知：所有满足条件的数可表示为12n-2，也就是除以12余2;所有12n-2中满足被5除余4：最小数是n=3时，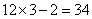

5、单选题  一个数被4除余1，被5除余2，被6除余3，这个数最小是几?_____
A: 10
B: 33
C: 37
D: 57
参考答案: D
本题解释:参考答案:D
题目详解:此题为剩余定理中差同的情况。根据"差同减差，最小公倍数做周期"可知：这个数加上3以后，为4、5、6的倍数;而4、5、6的最小公倍数为60：因此该数最小为