1、单选题  一直角三角形的两直角边的长度之和为14，假如这个三角形的周长与面积数值相等，那么该三角形的面积为_____。
A: 20
B: 22.5
C: 24
D: 24.5
参考答案: C
本题解释:正确答案是C考点几何问题解析

2、单选题  服装厂的工人每人每天可以生产4件上衣或7条裤子，一件上衣和一条裤子为一套服装。现有66名工人生产，每天最多能生产多少套服装?_____
A: 168
B: 188
C: 218
D: 246
参考答案: A
本题解释:正确答案是A考点鸡兔同笼问题解析由题意，每个工人每天可以生产的上衣和裤子的比例为4：7，要使生产的服装套数更多，则最终生产的上衣和裤子数量要相同，所以生产上衣和裤子的工人比例为7：4，有66名工人，则生产上衣的工人数量为66×7/11=42，生产裤子的工人数量为66×4/11=24，生产服装数量最多等于42×4=168。故正确答案为A。

3、单选题  一条双向铁路上有11个车站，相邻两站都相距7千米。从早晨7点，有18列货车由第11站顺次发出，每隔5分钟发一列，都驶向第一站，速度都是每小时60千米;早晨8点，由第1站发一列客车，向第11站驶出，时速100千米，在到达终点前，货车与客车都不停靠任何一站。那么，在_____，客车能与3列货车先后相遇。
A: 在第四、五站之间
B: 在第五、六站之间
C: 在第六、七站之间
D: 在第七、八站之间
参考答案: B
本题解释:正确答案是B考点行程问题解析铁路上共有11个站，相邻两站相距7千米，则共有70千米的距离，每辆货车之间的距离是5千米。早晨8点，第一列货车已经开出60千米，与第一站相距10千米。客车和第一辆货车相遇时行驶路程为6.25千米，之后每行驶3.125公里即相遇一列货车，则相遇点距第一站点的距离是6.25+3.125n。要使客车在两个站点之间与连续3列货车相遇，则这三列货车中的第一列与客车相遇的地点距离站点不超过：7-3.125×2=0.75千米。即6.25+3.125n除以7余数<0.75，取n=7时商为4，余数为0.125<0.75。则客车行驶在第五、六站之间，分别和第8、9、10辆货车相遇。故正确答案为B。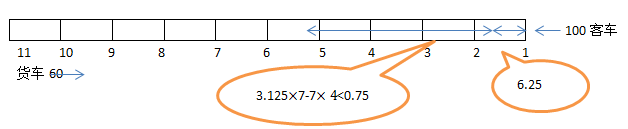

4、单选题  如图，在单位网格纸上有一个三角形，这个三角形的面积是_____。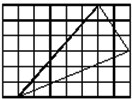A: 13.5平方单位
B: 15.5平方单位
C: 17.5平方单位
D: 19.5平方单位
参考答案: A
本题解释:正确答案是A考点几何问题解析总面积为8×6=48，外部面积为1×6+5×6÷2+7×3÷2+3×2÷2=34.5，故三角型面积=48-34.5=13.5。故正确答案为A。

5、单选题  用2、3、4、5、6、7六个数字组成两个三位数，每个数字只用一次，这两个三位数的差最小是多少?_____
A: 47
B: 49
C: 69
D: 111
参考答案: A
本题解释:正确答案是A考点多位数问题解析因为每个数字只能用一次，显然首位决定大小，因此三个三位数的百位数字至少相差1，在这种情况下要使差值最小，则两个三位数为最接近，从而可知较小的三位数之末两位应尽可能大，而较大的三位数之末两位应尽可能小。在这个思想下，可知合适的三位数情况构造为523、476，此时三位数之末两位的差距最大，从而差值最小，最小差值为47。故正确答案为A。