1、单选题  一只木箱内有白色乒乓球和黄色乒乓球若干个。小明一次取出5个黄球、3个白球，这样操作N次后，白球拿完了，黄球还剩8个;如果换一种取法：每次取出7个黄球、3个白球，这样操作M次后，黄球拿完了，白球还剩24个。问原来木箱内共有乒乓球多少个?_____
A: 246个
B: 258个
C: 264个
D: 272个
参考答案: C
本题解释:参考答案:C本题得分:
题目详解:“小明一次取出5个黄球、3个白球，这样操作N次后，白球拿完了，黄球还剩8个”，即：第一次取出8N个还剩8个，那么总数肯定能被8整除;“每次取出7个黄球、3个白球，这样操作M次后，黄球拿完了，白球还剩24个”，即：第二次取出10M个还剩24个，那么尾数只能是4;所以，选C。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除的性质

2、单选题  一篇文章，现有甲、乙、丙三人，如果由甲乙两人合作翻译，需要10小时完成；如果由乙丙两人合作翻译，需要12小时完成；现在先由甲丙两人合作翻译4小时，剩下的再由乙单独翻译，需要12小时才能完成。则这篇文章如果全部由乙单独翻译，需要_____小时能够完成。
A: 15  
B: 18  
C: 20 
D: 25
参考答案: A
本题解释:【答案】A。解析：设总的工作量为1，则甲乙两人的工作效率和为，乙丙两人的工作效率和为。现在甲丙合作4小时，乙单独工作12小时的工作量，相当于甲乙合作4小时，乙丙合作4小时，乙再单独工作4小时的工作量。则乙工作4小时的工作量为1-×4－×4＝，即乙每小时的工作量为，所以乙需要15小时完成工作。

3、单选题  某礼堂的观众座椅共96张，分东、南、西三个区域摆放。现从东区搬出与南区同样多的座椅放倒南区，再从南区搬出与西区同样多的座椅放到西区，最后从西区搬出与东区剩下的座椅数量相同的座椅放到东区，这时三个区域的座椅数量相同。则最初南区的座椅有_____张。
A: 24
B: 28
C: 32
D: 36
参考答案: B
本题解释:正确答案是B考点统筹规划问题解析第一次搬：东-南，2南，西;第二次搬：东-南，2南-西，2西;第三次搬：2东-2南，2南-西，2西-东+南。2东-2南=2南-西=2西-东+南，解得4南=7西，则南区座椅数肯定为7的倍数，只有B符合条件。故正确答案为B。标签数字特性

4、单选题  连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米，则正八面体的体积为_____立方厘米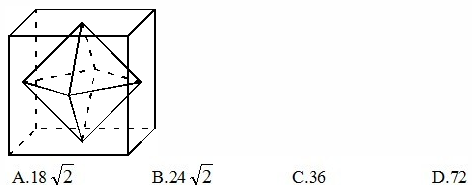A: A
B: B
C: C
D: D
参考答案: C
本题解释:正确答案是C考点几何问题解析

5、单选题  两辆汽车同时从某地出发到同一目的地，路程180千米。甲车比乙车早到0.8小时。当甲车到达目的地时，乙车离目的地32千米。甲车行驶全程用了_____小时。
A: 3.5
B: 3.7
C: 4
D: 4.5
参考答案: B
本题解释:【解析】乙车的来源:91考试网速度为32÷0.8=40千米/小时，则乙车行驶全程用了180÷40=4.5/小时，故甲行驶全程用了4.5-0.8=3.7小时。