1、单选题  甲、乙两辆清洁车执行东、西城间的公路清扫任务。甲车单独清扫需要6小时，乙车单独清扫需要9小时，两车同时从东、西城相向开出，相遇时甲车比乙车多清扫15千米。问东、西两城相距多少千米?_____
A: 60千米
B: 75千米
C: 90千米
D: 135千米
参考答案: B
本题解释:正确答案是B考点工程问题解析甲乙的速度比为3：2，设全程为5份，则甲乙相遇时甲清扫了3份，乙清扫了2份，甲比乙多1份，而1份对应15千米，因此东西两城相距5×15=75千米。标签赋值思想比例转化

2、单选题  甲、乙各有钱若干元，甲拿出1/3给乙后，乙再拿出总数的1/5给甲，这时他们各有160元，问甲、乙原来各有多少钱?_____
A: 120元200元
B: 150元170元
C: 180元140元
D: 210元110元
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析解析1：乙拿出1/5给甲后甲乙各有160元，说明之前乙有160÷4/5=200元，甲有120元，这是甲给乙1/3后剩余的钱数，则甲原有120÷2/3=180元，乙有200-60=140元。解析2：设甲乙原有钱分别为x、y，根据题意有，2/3x+1/5(1/3x+y)=160，4/5(1/3x+y)=160，解得x=180，y=140。标签直接代入逆向考虑

3、单选题  _____ A: A
B: B
C: C
D: D
参考答案: B
本题解释:正确答案是B考点几何问题解析因为正三角形的周长和正六边形的周长相等，又因为正三角形和正六边形的边长的个数比是1：2，所以其边长之比为2：1，假设正三角形的边长为2，则正六边形的边长为1。正六边形可以分成6个小正三角形，如下图所示，边长为1的小正三角形面积：加长为2的正三角形面积=1：4。所以正六边形面积：正三角形面积=6：4=1.5，故正确答案为B。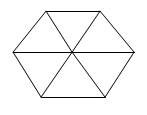

4、单选题  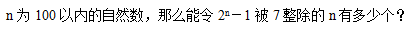_____ A: 32
B: 33
C: 34
D: 35
参考答案: B
本题解释:正确答案是B考点余数与同余问题解析

5、单选题  有一艘船，出现了一个漏洞，水以均匀的速度进入船内。发现漏洞时，已进入一些水，如果由12人淘水，3小时可以淘完，如果只有5人淘水，要10小时才能淘完，现在想用2小时淘完，需用多少人淘水?_____
A: 17
B: 16
C: 15
D: 18
参考答案: A
本题解释:正确答案是A考点牛吃草问题解析假设发现漏水时船上已进水为N，每分钟进水为Y，根据题意可得N=(12-Y)×3，N=(5-Y)×10，解得N=30，Y=2。因此若两个小时淘完，需要30÷2+2=17人。故正确答案为A。公式：在牛吃草模型背景下，公式为N=(牛数-Y)×天数，其中N表示原有草量的存量，以牛数与天数的乘积来衡量;Y表示专门吃新增加草量所需要的牛数。标签公式应用