1、单选题  一厂家生产销售某新型节能产品。产品生产成本是168元，销售定价为238元。一位买家向该厂家预订了120件产品，并提出产品销售价每降低2元，就多订购8件。则该厂家在这笔交易中能获得的最大利润是_____元。
A: 17920
B: 13920
C: 10000
D: 8400
参考答案: C
本题解释:正确答案是C考点函数最值问题解析假设下降m元，等到最大利润，则有(238-168-m)×(120+m÷2×8)=(70-m)×(120+4m)=(70-m)×(m+30)×4，当m+30=70-m时，求得最大值，此时m=20，则最大利润为50×50×4=10000。故正确答案为C。

2、单选题 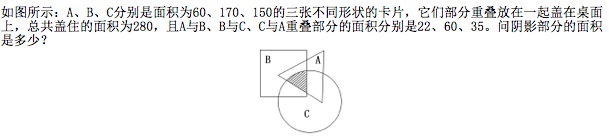 A: 15
B: 16
C: 17
D: 18
参考答案: C
本题解释:正确答案是C考点容斥原理问题解析套用三集合容斥原理公式，60+170+150-22-60-35+X=280，根据尾数法知答案为C。三集合容斥原理公式：|A∪B∪C|=|A|+|B|+|C|-|A∩B|-|B∩C|﹣|C∩A|+|A∩B∩C|。

3、单选题  玉米的正常市场价格为每公斤1.86元到2.18元，近期某地玉米的价格涨至每公斤2.68元。经测算，向市场每投放储备玉米100吨，每公斤玉米价格可下降0.05元。为稳定玉米价格，向该地投放储备玉米的数量不能超过_____。
A: 800吨
B: 1080吨
C: 1360吨
D: 1640吨
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析所求量为投放储备玉米的最大数量，对应正常市场价格的最低价。此时价格差为2.68-1.86=0.82元，而每100吨可降0.05元，因此数量不能超过0.82÷0.05×100=1640吨。故正确答案为D。

4、单选题  某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位，甲教室每排可坐10人，乙教室每排可坐9人。两教室当月共举办该培训27次，每次培训均座无虚席，当月培训1290人次。问甲教室当月共举办了多少次这项培训?_____
A: 8
B: 10
C: 12
D: 15
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析乙教室可坐9人，可知乙培训过的人数含有因子3，而总的培训人数1290也含有因子3，因此甲教室培训过的人数也必然含有3因子。而甲教室可坐50人，因此要使甲教室培训过的人数也含有3因子，则其举办次数必然含有3因子，因此只有C、D符合。将C选项代入，可知此时乙教室举办过15次培训，其总人数的尾数为5，而甲教室培训的总人数尾数总是为0，因此甲、乙教室的培训人数尾数为5，不符合要求。故正确答案为D。秒杀技由题意，甲教室每次培训50人，乙教室每次培训45，假设甲乙的次数分别为X、Y，则可得50X+45Y=1290，观察等式可知45Y的尾数必然为0，因此Y必然为偶数，从而X为奇数，仅D符合。故正确答案为D。

5、单选题  某市一条大街长7200米，从起点到终点共设有9个车站，那么每个车站之间的平均距离是_____。
A: 780米
B: 800米
C: 850米
D: 900米
参考答案: D
本题解释:正确答案是D考点计数模型问题解析该问题为计数模型中的植树问题。车站间的平均距离为7200÷(9-1)=900。故正确答案为D。