1、单选题  一列长90米的火车以每秒30米的速度匀速通过一座长1200米的桥，所需时间_____秒。
A: 37
B: 40
C: 43
D: 46
参考答案: C
本题解释:正确答案是C考点行程问题解析所需时间为(1200+90)÷30=43秒。故正确答案为C。

2、单选题  在1000以内，除以3余2，除以7余3，除以11余4的数有多少个?_____
A: 4
B: 5
C: 6
D: 7
参考答案: B
本题解释:正确答案是B考点余数与同余问题解析同余问题，不符合“余同取余，和同加和，差同减差，最小公倍数做周期”的口诀，通过余数组获得通式。除以3余2的余数组为2、5、8、11、14、17、···;除以7余3的余数组为3、10、17、···。结合此两者可知满足前两条的被除数可写成21n+17，其余数组为17、38、59、···;而除以11余4的余数组为4、15、26、37、48、59、···。结合此两者可知满足三条的被除数可写成231n+59。由题意：0≤231n+59≤1000，解得0≤n≤4。所以这样的数共有5个，故正确答案为B。口诀解释：余同取余，例如“一个数除以7余1，除以6余1，除以5余1”，可见所得余数恒为1，则取1，被除数的表达式为210n+1;和同加和，例如“一个数除以7余1，除以6余2，除以5余3”，可见除数与余数的和相同，取此和8，被除数的表达式为210n+8;差同减差，例如“一个数除以7余3，除以6余2，除以5余1”，可见除数与余数的差相同，取此差4，被除数的表达式为210n-4。特别注意前面的210是5、6、7的最小公倍数。

3、单选题  一只油轮从甲港顺流而下到乙港，马上又逆水返回甲港，共用8小时，顺水每小时比逆水每小时多行12千米，前4小时比后4小时多行30千米，则甲、乙两港相距_____千米。
A: 72
B: 60
C: 55
D: 48
参考答案: C
本题解释:【解析】由于顺水速度大于逆水速度。且顺水、逆水的行程相等，则顺水时间小于逆水时间，后4/小时全是逆水，前4小时先是顺水后是逆水，顺水时间=30÷12=2.5小时，逆水时间=8-2.5=5.5/小时，故顺水速度：逆水速度=5.5：2.5=11：5，顺水速度=12÷（11.-5）×11=22千米/时，两港距离=22×2.5=55（千米）。故选C。

4、单选题 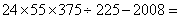 A: 168
B: 172
C: 184
D: 192
参考答案: D
本题解释:参考答案
题目详解:<暂无>考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分

5、单选题  往一个圆柱形容器里注水，已知容器底面半径为10cm，高为40cm，当注入水柱高为H，水柱高由低到高变化时，水柱体积V(cm&sup2;)也随之发生变化，下列说法中，不正确的是_____。
A: V与H都是变量
B: H是自变量，V是因变量
C: V与H的关系可为V=100πH
D: V=150立方厘米时，H=25厘米
E: 当H是40厘米时，V达到最大值为4000π，此时不能再注入水
参考答案: D
本题解释:正确答案是D考点几何问题解析