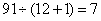1、单选题  先将线段AB分成20等分，线段上的等分点用“△”标注，再将该线段分成21等分，等分点用“O”标注(AB两点都不标注)，现在发现“△”和“O”之间的最短处为2厘米，问线段AB的长度为多少?_____
A: 2460厘米
B: 1050厘米
C: 840厘米
D: 680厘米
参考答案: C
本题解释:参考答案:C
题目详解:解法一：前后两次段数的最小公倍数是：20×21=420，再由“△”和“O”之间的最短长度只可能发生在线段AB的两端，且“△”和“O”之间的最短处为2厘米，则：AB=20×21×2=840cm。所以，选C。解法二：两种不同标号间的最短距离为：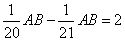

2、单选题  有苹果，桔子各一筐，苹果有240个，桔子有313个，把这两筐水果平均分给一些小朋友，已知苹果分到最后余2个，桔子分到最后还余7个，求最多有多少个小朋友参加分水果?_____
A: 14
B: 17
C: 28
D: 34
参考答案: D
本题解释:参考答案
题目详解:根据题意，由于苹果分到最后余2，桔子分到最后余7，那么：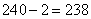

3、单选题  男女并排散步，女的3步才能跟上男的2步。两人从都用右脚起步开始到两人都用左脚踏出为止，女的应走出多少步?_____
A: 6步
B: 8步
C: 12步
D: 多少步都不可能
参考答案: A
本题解释:参考答案:A
题目详解:根据题意，即求2，3的最小公倍数;因为并排：那么男人走两步与女人走三步同速;首先男人前两步为：右脚--左脚，女人前三步为：右脚--左脚--右脚;等到男人后两步为：右脚--左脚，女人后三步为：左脚---右脚---左脚，此时与男人同时迈左脚出;女人一共走了6步。所以，选A。考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>两个数的最大公约数和最小公倍数

4、单选题  如图所示，街道ABC在B处拐弯，在街道一侧等距装路灯，要 求A、B、C处各装一盏路灯，这条街道最少装多少盏路灯?_____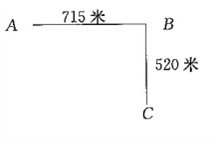A: 18
B: 19
C: 20
D: 21
参考答案: C
本题解释:参考答案:C
题目详解:根据题意，灯距应取715和520的最大公约数，即65米;则最少装路灯的数量为：(715+520)÷65+1=20盏。所以，选C考查点:数量关系>数学运算>计算问题之数的性质>公约数与公倍数问题>两个数的最大公约数和最小公倍数

5、单选题  6.有两个两位数，这两个两位数的最大公约数与最小公倍数的和是91，最小公倍数是最大公约数的12倍，求这较大的数是多少?_____
A: 42
B: 38
C: 36
D: 28
参考答案: D
本题解释:参考答案
题目详解:此题可以根据定义来解答。这两个数的最大公约数是：