1、单选题  某一学校有500人，其中选修数学的有359人，选修文学的有408人，那么两种课程都选的学生至少有多少?_____。
A: 165人
B: 203人
C: 267人
D: 199人
参考答案: C
本题解释:C【解析】若一人只选修一门课程，则至少有359+408=767(人)，但该学校只有500人，多出的767-500=267(人)则是选两门课程的。故正确答案为C。

2、单选题  同学们进行队列训练，如果每排8人，最后一排6人;如果每排10人，最后一排少4人。参加队列训练的学生最少有多少人?_____
A: 46
B: 54
C: 62
D: 66
参考答案: A
本题解释:参考答案:A
题目详解:每排10人，最后一排少4人，换种方式理解就是最后一排站了6人：因此此题是余数问题中余同的情况，"余同取余，最小公倍数做周期"可知：8和10的最小公倍数是40。因此，这些学生至少有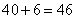

3、单选题  有黑、白、黄色袜子各10只，不用眼睛看，任意地取出袜子来，使得至少有两双袜子不同色，那么至少要取出_____只袜子。
A: 12
B: 13
C: 11
D: 14
参考答案: B
本题解释:【解析】考虑最坏的情形，把某一种颜色的袜子全部先取出，然后，在剩下两色袜子中各取出一只，这时再任意取一只都必将有两双袜子不同色，即10+2+l=13（只）。故选B。

4、单选题  甲、乙、丙三名运动员囊括了全部比赛项目的前三名，他们的总分分别是8、7和17分，甲得了一个第一名，已知各个比赛项目分数相同，且第一名的得分不低于二、三名得分的和，那么比赛共有多少个项目?_____
A: 3
B: 4
C: 5
D: 6
参考答案: B
本题解释:【答案解析】全部比赛前三名的总分为8+7+17=32分，每个项目前三名的分数和至少是3+2+1=6分，所以每个项目前三名的分数和应该是32的大于6的约数，只能是8、16、32;如果是16或32，因为甲得了一个第一，所以甲的得分应大于8，不合题意，所以每个项目前三名的分数和是8分，共有项目32÷8=4个。

5、单选题  某次数学竞赛共有10道选择题，评分办法是答对一道得4分，答错一道扣1分，不答得0分。设这次竞赛最多有，N种可能的成绩，则N应等于多少?_____
A: 45
B: 47
C: 49
D: 51
参考答案: A
本题解释:参考答案:A
题目详解:设答对