1、单选题  某招聘会在入场前若干分钟就开始排队，每分钟来的求职人数一样多，从开始入场到等候入场的队伍消失，同时开4个入口需30分钟，同时开5个入口需20分钟。如果同时打开6个入口，需多少分钟?_____
A: 8
B: 10
C: 12
D: 15
参考答案: D
本题解释:正确答案是D考点牛吃草问题解析假定原有人数N人，每分钟新增人数Y人，则可得：N=(4-Y)×30，N=(5-Y)×20，解得Y=2，N=60。将6个入口代入，可得所需时间为60÷(6-2)=15(分钟)。故正确答案为D。公式：在牛吃草模型背景下，公式为N=(牛数-Y)×天数，其中N表示原有草量的存量，以牛数与天数的乘积来衡量;Y表示专门吃新增加草量所需要的牛数。

2、单选题  一个边长为20的方阵，最外面三圈人数总和为多少?_____
A: 196
B: 204
C: 256
D: 324
参考答案: B
本题解释:参考答案:B
题目详解:方阵边长为20，总人数为400;除去最外面三圈人数，里面的小方阵边长为：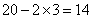

3、单选题  12个啤酒空瓶可以免费换1瓶啤酒，现有101个啤酒空瓶，最多可以免费喝到的啤酒为_____。
A: 10瓶
B: 11瓶
C: 8瓶
D: 9瓶
参考答案: D
本题解释:正确答案是D考点计数模型问题解析根据题意可知，12个空瓶换1瓶酒，12空瓶=1空瓶+1酒，因此题意等价于11空瓶=1酒，而101÷11=9……2，即可换9瓶酒。故答案为D。

4、单选题  有一路电车从甲站开往乙站，每五分钟发一趟，全程走15分钟。有一人从乙站骑自行车沿电车线路去甲站。出发时，恰好有一辆电车到达乙站，在路上他又遇到10辆迎面开来的电车，到站时恰好有一辆电车从甲站开出，那么，他从乙站到甲站共用多少分钟?_____
A: 40
B: 6
C: 48
D: 45
参考答案: A
本题解释:正确答案是A考点行程问题解析当编号为A1的第一辆车到达乙站时，编号为A4的第四辆车恰好刚从甲站出发，假设骑车人刚从乙站出发时，编号为A1的第一辆车到达乙站，则途中骑车人又遇到了10辆车，则当他到达甲站时，恰好编号为A12的第十二辆车从甲站开出，而此时编号为A9的第九辆车刚刚到达乙站，显然，电车从A1到A9所用的时间也恰是骑车人用的时间，所以答案为(9-1)×5=40分钟。正确答案选A。

5、单选题  如图所示，正方形ABCD条边的中点分别为E、F、G和H。问图中一共有多少个三角形？_____
A: 36
B: 40
C: 44
D: 48
参考答案: C
本题解释:正确答案是C解析分类来数，小三角形：16个；由两个小三角形组成的三角形：4×4＝16个；由四个小三角形组成的三角形：4＋4＝8个；由8个小三角形组成的三角形：4个；共16＋16＋8＋4＝44个，故正确答案为C。趣味数学问题