1、单选题  如图，在单位网格纸上有一个三角形，这个三角形的面积是_____。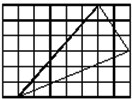A: 13.5平方单位
B: 15.5平方单位
C: 17.5平方单位
D: 19.5平方单位
参考答案: A
本题解释:正确答案是A考点几何问题解析总面积为8×6=48，外部面积为1×6+5×6÷2+7×3÷2+3×2÷2=34.5，故三角型面积=48-34.5=13.5。故正确答案为A。

2、单选题  在自然数1至50中，将所有不能被3除尽的数相加，所得的和是_____。
A: 865
B: 866
C: 867
D: 868
参考答案: C
本题解释:正确答案是C考点数列问题解析”1至50，所有不能被3除尽的数相加”，等价于”1到50所有数的和减去能被3整数的项”，所以代求的值为(1+2+……50)-(3+6+……+48)=50×51/2-3×16×17/2=1275-408=867，故正确答案为C。秒杀技”1到50所有数的和”能被3整除，减去所有能被3整除的数后，还能被3整除。所以”不能被3除尽的数的和”能被3整除，选项中只有C满足，故正确答案为C。

3、单选题  如右图所示，正方形ABCD的边长为5cm，AC、BD分别是以点D和点C为圆心、5cm为半径作的圆弧。问阴影部分a的面积比阴影部分b小_____。(π取3.14)
参考答案: B

4、单选题  林子里的猴子喜欢吃的野果，23只猴子可以在9周内吃光，21只猴子可以在12周内吃光，问如果有33只猴子一起吃，则需要几周吃光(假定野果生长的速度不变)?_____
A: 2周
B: 3周
C: 4周
D: 5周
参考答案: C
本题解释:正确答案是C考点牛吃草问题解析设原有野果为N，每周生长的野果可供Y个猴子吃，根据题意可得：N=(23-Y)×9，N=(21-Y)×12，解得N=72，Y=15。因此若33只猴子一起吃，需要时间为72÷(33-15)=4周。故正确答案为C。公式：在牛吃草模型背景下，公式为N=(牛数-Y)×天数，其中N表示原有草量的存量，以牛数与天数的乘积来衡量;Y表示专门吃新增加草量所需要的牛数。标签公式应用

5、单选题  甲、乙两人卖数量相同的萝卜，甲打算卖1元2个，乙打算卖1元3个。如果甲乙两人一起按2元5个的价格卖掉全部的萝卜，总收入会比预想的少4元钱。问两人共有多少个萝卜?_____
A: 420
B: 120
C: 360
D: 240
参考答案: D
本题解释:正确答案是D考点经济利润问题解析设原来的萝卜共有a个，则每个人都有a/2个萝卜，根据题意有：(1/2×a/2+1/3×a/2)-2a/5=4，解得a=240，故正确答案为D。秒杀技由题意可知甲打算15元30个，乙打算10元30个，即25元60个。合在一起则为24元60个，也即每60个萝卜少卖1元，因此少卖4元应为240个，这里的30的由来是从2、3、5的最小公倍数想到的。