1、单选题  某班有60名学生，在第一次测验中有32人得满分，在第二次测验中有27人得满分。如果两次测验中都没有得满分的学生有17人，那么两次测验中都获得满分的人数是多少?_____
A: 13人
B: 14人
C: 15人
D: 16人
参考答案: D
本题解释:正确答案是D考点容斥原理问题解析本题注意按照得满分得到两个类，进行容斥原理分析。设第一次测验得满分为事件A，第二次测验得满分为事件B，则两次都得满分为A∩B，将其设为x人，得过满分为A∪B。根据公式A∪B=A+B-A∩B可得：60-17=32+27-x解得x=16，因此两次测验中都获得满分的人数是16人，故正确答案为D。

2、单选题  建华中学共有1600名学生，其中喜欢乒乓球的有1180人，喜欢羽毛球的有1360人，喜欢篮球的有1250人，喜欢足球的有1040人，问以上四项球类运动都喜欢的至少有几人?_____
A: 20人
B: 30人
C: 40人
D: 50人
参考答案: B
本题解释:正确答案是B考点抽屉原理问题解析采取逆向思维法。不喜欢乒乓的1600-1180=420，不喜欢羽毛球的1600-1360=240，不喜欢篮球的1600-1250=350，不喜欢足球的1600-1040=560，要使四项运动都喜欢的人数最少，那么不喜欢的人数就要最多那么都尽量不相交，从而达到最多：420+240+350+560=1570人，所以喜欢的最少的为1600-1570=30人，故正确答案为B。

3、单选题  在空间中最多能放置多少个正方体，使得任意两个正方体都有一部分表面相接触?_____
A: 4
B: 5
C: 6
D: 7
参考答案: A
本题解释:正确答案是A考点几何问题解析注意到一个立方体的六个面，形成3组相对面，而一组相对面上不可能同时贴有立方体，因此一个立方体周围最多可以贴3个立方体，故最多能放置4个立方体，使得任意两个立方体均有部分表面相接触。下图即为一个示例：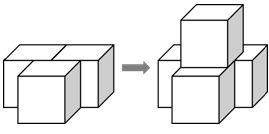

4、单选题  办公室有甲、乙、丙、丁4位同志，甲比乙大5岁，丙比丁大2岁。丁三年前参加工作，当时22岁。他们四人现在的年龄之和为127岁。那么乙现在的年龄是_____。
A: 25岁
B: 27岁
C: 35岁
D: 40岁
参考答案: C
本题解释:正确答案是C考点年龄问题解析丁3年前22岁，则现在25岁，丙比丁大2岁，丙现在27岁，甲、乙年龄和为127-(25+27)=75岁，甲比乙大5岁，则乙现在的年龄是(75-5)÷2=35岁。故正确答案为C。

5、单选题  某单位举办庆国庆茶话会，买来4箱同样重的苹果，从每箱取出24千克后，结果各箱所剩的苹果重量的和，恰好等于原来一箱的重量。那么原来每箱苹果重多少千克?_____
A: 16
B: 24
C: 32
D: 36
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析解析1：设原来每箱苹果重x千克，根据题意可得：4(x-24)=x，解得x=32，故选择C选项。解析2：原来一共4箱苹果，由“从每箱取出24千克后，结果各箱所剩的苹果重量的和，恰好等于原来一箱的重量”，可知总共取出来的苹果重量是原来3箱苹果的重量，因此原来每箱苹果的重量为：24×4÷3=32，故选择C选项。