1、单选题  某校按字母A到Z的顺序给班级编号，按班级编号加01、02、03……，给每位学生按顺序定学号，若A～K班级人数从15人起每班递增1名，之后每班按编号顺序递减2名，则第256名学生的学号是多少?_____
A: M12
B: N11
C: N10
D: M13
参考答案: D
本题解释:正确答案是D考点多位数问题解析此题对应数列呈先升后降趋势，根据题意可明确给出班级人数数列，待求第256名学生的位置，由题意知A班有15人，B班有16人，……，递增到K班25人，然后L班23人，逐班减少。结合四个选项可知，第256名学生不是在M班，就是在N班，此即帮助限定范围，于是直接计算从A班到L班的学生总数为15+16+……+25+23=(15+25)÷2×11+23=243(人)，距离256为13，可知第256名学生的学号为M13，故正确答案为D。

2、单选题  甲、乙两人由于顺路搭乘同一辆出租车，甲做了4公里后下了车，出租车又走了6公里，乙下车并付了18元车费，如果由两人分摊，甲应分摊多少元?_____
A: 3元
B: 3.6元
C: 7.2元
D: 7.5元
参考答案: B
本题解释:正确答案是B考点行程问题解析因为出租车一共行驶10公里，车费18元，所以每公里车费为1.8元，因此前4公里车费为4×1.8=7.2元，所以甲应支付7.2/2=3.6元。故正确答案为B。

3、单选题  有20人修筑一条公路，计划15天完成。动工3天后抽出5人植树，留下的人继续修路。如果每人工作效率不变，那么修完这段公路实际用多少天?_____
A: 16
B: 17
C: 18
D: 19
参考答案: D
本题解释:正确答案是D考点行程问题解析设工程总量为300，20人修筑该公路，计划15天完成，则每人每天的工作量为1，动工3天后抽出5人植树，20人修3天完成了：20×3=60，那么总工作量还剩下：300-60=240，这些剩下的工作给15人做，并且每人每天的工作量保持不变，那么就还需要工作：240÷15=16天，实际工作就有：3+16=19，故正确答案为D。秒杀技人数变为原来的3/4，则完成时间变为原来的4/3，即(15-3)×4/3=16，因此实际工作就有16+3=19，故选择D选项。标签赋值思想比例转化

4、单选题  一小型货车站最大容量为50辆车，现有30辆车，已知每小时驶出8辆，驶入10辆，则多少小时车站容量饱和?_____
A: 8
B: 10
C: 12
D: 14
参考答案: B
本题解释:正确答案是B考点和差倍比问题解析因为每小时驶出8辆，驶入10辆，所以每小时车站增加10-8=2辆车，所以时间为(50-30)÷2=10小时。故正确答案为B。

5、单选题  如下图所示，AB两点是圆形体育场直径的两端，两人从AB点同时出发，沿环形跑道相向匀速而行，他们在距A点弧形距离80米处的C点第一次相遇，接着又在距B点弧形距离60米处的D点第二次相遇，问这个圆形体育场的周长是多少米?_____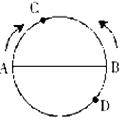A: 240
B: 300
C: 360
D: 420
参考答案: C
本题解释:正确答案是C考点行程问题解析解析1：根据题意可知两人第一个运动过程的路程和为半个圆周，第二个运动过程的路程和为整个圆周，因此每个人在两个过程中的路程比为1：2，设劣弧BC长为x，根据题意可得，80：(x+60)=1：2，解得x=100，因此圆周长为：2×(80+100)=360，故正确答案为C。解析2：此题为两次相遇问题，运用公式可得圆周长的一半为：80×3-60=180米，因此周长为360米，故正确答案为C。备注：两次相遇问题，两边型的两端点之间的距离公式：S=3A-B，其中S表示两端点之间的距离，A、B表示先后两次相遇点分别关于两个端点的距离。