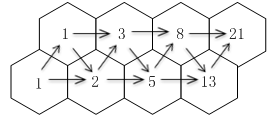
1、单选题  将半径分别为4厘米和3厘米的两个半圆如图放置，则阴影部分的周长是_____。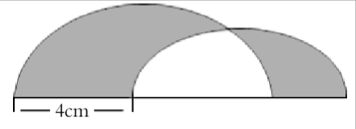A: 21.98厘米
B: 27.98厘米
C: 25.98厘米
D: 31.98厘米
参考答案: B
本题解释:正确答案是B考点几何问题解析阴影部分左侧底边长度为大圆半径4cm，右侧底边长度为大圆半径加小圆直径再减去大圆直径，为4+6-8=2cm，阴影部分周长为两个半圆的周长加上左右两个底边的长度，周长=πR+πr+4+2=3.14×7+6=27.98cm，故正确答案为B。

2、单选题  A: ①
B: ①②
C: ②③
D: ①③
参考答案: D
本题解释:正确答案是D考点几何问题解析两三角形全等的判定：两边和夹角分别相等才是全等三角形。①符合边角边定理，正确;②为边边角，不符合，错误;③为边角边，符合，正确。即①③正确，故正确答案为D。

3、单选题  下图是一个奥林匹克五环标志。这五个环相交成9部分：A、B、C、D、E、F、G、H、I。请将数字1、2、3、4、5、6、7、8、9分别填入这9个部分中，使得五环内的数字之和恰好构成五个连续的自然数。那么，这五个连续自然数的和的最大值是多少?_____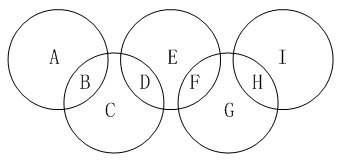A: 65
B: 75
C: 70
D: 102
参考答案: C
本题解释:正确答案是C考点趣味数学问题解析因为B、D、F、H同时出现在两个圆圈中而其他数都出现在一个圆圈中，所以五个圆圈中的总和为1+2+3+……+9+B+D+F+H≤45+9+8+7+6=75。若五个圆圈中的总和为75，则B+D+F+H=9+8+7+6=30，又因为五个环内的数字和恰好构成五个连续的自然数，所以这五个环内的数字只能是13、14、15、16、17，考虑两端两个圆圈中的总和，S=(A+B)+(H+I)≥13+14=27，但B+H≤9+8=17，A+I≤4+5=9，所以S最大为26，与上面的结论矛盾，所以五个圆圈中的总和不可能为75，又因为五个连续自然数的和是5的倍数，所以五个圆圈中的总和最大为70。当(A、B、C、D、E、F、G、H、I)=(9、7、3、4、2、6、1、8、5)时，五个圆圈的总和就可以取到70，故正确答案为C。

4、单选题  现有6个一元面值硬币正面朝上放在桌子上，你可以每次翻转5个硬币(必须翻转5个)，问你最少经过几次翻转可以使这6个硬币全部反面朝上?_____
A: 5次
B: 6次
C: 7次
D: 8次
参考答案: B
本题解释:正确答案是B考点统筹规划问题解析将6个硬币抽象成一个6位二进制数字，假设硬币正面朝上时记为0，硬币反面朝上时记为1，因此原问题转化成每次改变5位数字，最少经过几次可以将000000变为111111的问题，按照顺序改变，第几次改变就让第几个不变，过程为：开始0：000000→变1次：011111→2：110000→3：000111→4：111100→5：000001→6：111111，因此总共需要6次，故选择B选项。标签构造调整

5、单选题 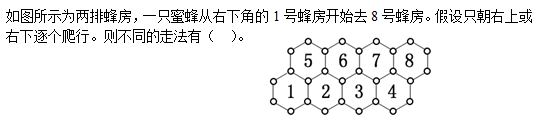 A: 16种
B: 18种
C: 21种
D: 24种
参考答案: D
本题解释:正确答案是D考点排列组合问题解析到达右下角的走法等于到达其正左侧蜂房方法数与到达其左上蜂房方法数之和，到达右上角的走法等于到达其正左侧蜂房方法数与到达其左下蜂房数之和。据此从左下角出发，按照右上角-右下角-右上角······-右上角的顺序，依次标出从1号蜂房出发到8号蜂房的方法数，如下图所示。