1、单选题  在一个老年活动中心，会下象棋的有59人，会下围棋的有48人，两种棋都不会下的有12人，两种棋都会下的有30人，问这个俱乐部一共有多少人?_____
A: 89人
B: 107人
C: 129人
D: 137人
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析根据两集合容斥原理，设该俱乐部总人数为a，则59+48-30=a-12，解得a=89(人)，故正确答案为A。注：两集合容斥原理推论公式：满足条件1的个数+满足条件2的个数-都满足的个数=总数-都不满足的个数。

2、单选题  有3个单位共订300份《人民日报》，每个单位最少订99份，最多101份。问一共有多少种不同的订法?_____
A: 4
B: 5
C: 6
D: 7
参考答案: D
本题解释:正确答案是D考点排列组合问题解析由“每个单位最少订99份，最多101份”可知，该问题分为两类，第一类是三个单位订报纸数分别为：99、100和101，此时对三个单位进行全排列共有订法：3×2×1=6;第二类是三个单位订报纸数分别为：100、100和100，此时只有1种订法，因此总共有订法：6+1=7，故正确答案为D。标签分类分步

3、单选题 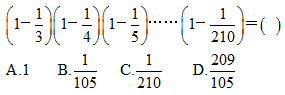 A: A
B: B
C: C
D: D
参考答案: B
本题解释:正确答案是B解析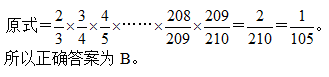

4、单选题  一批零件，如果第一天甲做，第二天乙做，这样交替轮流做，完成的天数恰好是整数。如果第一天乙做，第二天甲做，这样交替轮流做，做到上次轮流完成时所用的天数后，还剩40个不能完成，已知甲、乙工作效率的比是7：3。则甲每天做_____。
A: 30个
B: 40个
C: 70个
D: 120个
参考答案: C
本题解释:正确答案是C考点工程问题解析由题意，甲、乙两个人的工作效率为7：3，甲比乙每天多做4X个，两个轮流方式用时相等，但是第一种轮流方式做的零件数比第二种方式多，因此a为奇数(若a为偶数，两种方式完成的零件个数会相等)，所以在第一种方式中，最后一天做的是甲，甲|乙|甲…|甲，完成需要a天，第二种方式中最后一天做的是乙，乙|甲|乙…|乙，a天后还有40个没有完成，4X=40，X=10，甲每天做7X=7×10=70(个)。因此正确答案为C。

5、单选题  某产品售价为67.1，在采用新技术生产节约10%成本之后，售价不变，利润可可比原来翻一番。则该产品最初的成本为_____元。
A: 51.2
B: 54.9
C: 61
D: 62.5
参考答案: C
本题解释:正确答案：C节约的10%成本为增加的利润，利润翻一番为原先的2倍，则最初利润为成本的10%，最初的成本为67.1÷（1+10%=61元。