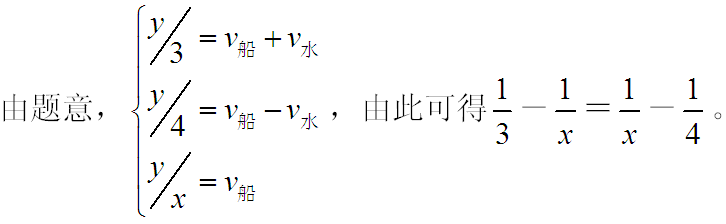1、单选题  有两种电话卡：第一种每分钟话费0.3元，除此以外，无其他费用;第二种电话卡，每分钟0.2元，另有每月固定费用10元(无论拨打与否都要扣)。如果小王每月通话量不低于两个小时，则他办理哪种卡比较合算?_____
A: 第一种
B: 第二种
C: 两个卡一样
D: 无法判断
参考答案: B
本题解释:正确答案是B考点分段计算问题解析设小王每月通话量m分钟，则m>120，使用第一种电话卡费用为0.3×m，使用第二种电话卡费用为10+0.2m，因为0.3m-0.2m-10=0.1m-10>0.1×120-10>0，所以第一种电话卡费用更高。故正确答案为B。

2、单选题  三位数的自然数N满足：除以6余3，除以5余3，除以4也余3，则符合条件的自然数N有几个?_____
A: 8
B: 9
C: 15
D: 16
参考答案: C
本题解释:正确答案是C考点余数与同余问题解析由题意可知满足同余情形，例如此题”三位自然数N除以6余3，除以5余3，除以4也余3”，可见余数恒为3，则取3，因此N的表达式为60n+3，其中60为6、5、4的最小公倍数，根据题目中的N为三位数，可得不等式100≤60n+3≤999，解得2≤n≤16，因此符合条件的自然数有15个，故正确答案为C选项。注：同余问题需要如下口诀：余同取余，和同加和，差同减差，最小公倍数做周期。口诀解释：余同取余，例如本题，余数恒为3，则取3;合同加和，例如”一个数除以7余1，除以6余2，除以5余3”，可见除数与余数的和相同，取此和8，被除数的表达式为210n+8;差同减差，例如”一个数除以7余3，除以6余2，除以5余1”。可见除数和余数的差相同，取此差4，被除数的表达式为210-4，其中210为5、6、7的最小公倍数。秒杀技根据题目，符合要求的数出现的周期为6、5、4的最小公倍数60，也即每60个连续自然数中必然有一个符合要求，三位数共有900个，因此符合要求的三位数共有900÷60=15(个)，故正确答案为C选项。标签最小公倍数同余问题

3、单选题 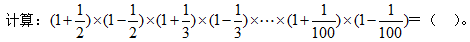 A: 101/100
B: 101/200
C: 101/300
D: 201/400
参考答案: B
本题解释:正确答案是B考点计算问题解析

4、单选题  某人以八五折的优惠购买一辆自行车节省60元，他实际付款_____元。
A: 350
B: 380
C: 400
D: 340
参考答案: D
本题解释:正确答案是D考点经济利润问题解析根据题意，自行车的原价为：60÷15%=400，所以实际付款额为：400-60=340元。故正确答案为D。

5、单选题  某旅游部门规划一条从甲景点到乙景点的旅游线路，经测试，旅游船从甲到乙顺水匀速行驶需3小时;从乙返回甲逆水匀速行驶需4小时，假设水流速度恒定，甲乙之间的距离为y公里，旅游船在静水中匀速行驶y公里需x小时，则x满足的方程为_____。A: A
B: B
C: C
D: D
参考答案: D
本题解释:正确答案是D考点行程问题解析