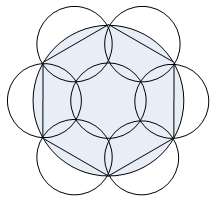
1、单选题  _____ A: A
B: B
C: C
D: D
参考答案: C
本题解释:正确答案是C考点几何问题解析

2、单选题  把一根钢管锯成5段需要8分钟，如果把同样的钢管锯成20段需要多少分钟?_____
A: 32分钟
B: 38分钟
C: 40分钟
D: 152分钟
参考答案: B
本题解释:正确答案是B考点计数模型问题解析锯成5段需要锯4次，即每次需要2分钟，而锯20段需要锯19次，因此需要：19×2=38分钟，故正确答案为B。

3、单选题  有一条新修的道路，现在需要在该道路的两边植树，已知路长为5052米，如果每隔6米植一棵树，那么一共需要植多少棵树?_____
A: 1646
B: 1648
C: 1686
D: 1628
参考答案: C
本题解释:正确答案是C考点计数模型问题解析这是一个双边线性植树模型，根据基本公式，棵树=2×(5052÷6+1)=2×(842+1)=1686(棵)，故正确答案为C选项。注：双边线性植树，棵树=2×(路长÷间隔+1)。

4、单选题  甲、乙、丙三个班向希望工程捐赠图书，已知甲班有1人捐6册，有2人各捐7册，其余各捐11册，乙班有1人捐6册，有3人各捐8册，其余各捐10册，丙班有2人捐4册，6人各捐7册，其余人各捐9册。已知甲班捐书总数比乙班多28册，乙班比丙班多101册，各班捐书总数在400~550册之间。那么，甲、乙、丙三个班各有多少人?_____
A: 48、50、53
B: 49、51、53
C: 51、53、49
D: 49、53、51
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析甲班比丙班多28+101=129册，则甲班总数在529—550之间;甲班为6+2×7+11n=20+11n，多捐2册就能被11整除，所以甲班总数只能是548(550-2)或537，因此丙班是419或408;丙班为2×4+6×7+9m=50+9m，多捐4册就能被9整除。因此丙班捐了419本，则丙班有(419-50)÷9+8=49人，故正确答案为C。

5、单选题  一个半径为r的圆用一些半径为r/2的圆去覆盖，至少要用几个小圆才能将大圆完全盖住?_____
A: 5个
B: 6个
C: 7个
D: 8个
参考答案: C
本题解释:正确答案是C考点几何问题解析已知大圆半径为r，小圆半径为r/2，则4个小圆的面积恰好等于一个大圆的面积。为保证小圆尽可能的覆盖大圆，当4个小圆不重叠时，所覆盖大圆部分的面积必小于大圆自身面积，若用5个小圆覆盖大圆，因为小圆的直径等于大圆的半径，所以当5个小圆不重叠时，无法覆盖住大圆的圆周，而6个小圆则恰好盖住大圆圆周，此时中间空白处再加上1个小圆，可将大圆完全覆盖，所以共需要7个小圆，如下图所示。