1、单选题  商场的自动扶梯以匀速由下往上行驶，两个孩子在行驶的扶梯上上下走动，女孩由下往上走，男孩由上往下走，结果女孩走了40级到达楼上，男孩走了80级到达楼下。如果男孩单位时间内走的扶梯级数是女孩的2倍。则当该扶梯静止时，可看到的扶梯梯级有_____。
A: 40级
B: 50级
C: 60级
D: 70级
参考答案: C
本题解释:正确答案是C考点行程问题解析解析1：设女孩的速度为x，男孩为2x，扶梯的速度为y，根据题意可知男孩和女孩所用的时间相同，有x+y=2x-y，得x：y=2，即女孩的速度为扶梯的2倍，因此当女孩走了40级时扶梯走了20级，扶梯静止时有60级。因此正确答案为C。解析2：因为男孩单位时间内走的扶梯级数是女孩的2倍，所以男孩走80级的时间和女孩走40级的时间相等，由此可知他们两个乘电梯的时间相同，则电梯运行距离也相等，也即有如下两式：对于男孩：电梯长度=80-电梯运行距离;对于女孩：电梯长度=40+电梯运行距离。由此可知电梯长度为60，故正确答案为C。

2、单选题  晓美骑在马背上过河，他共有甲、乙、丙、丁4只马，甲过河要2分钟，乙过河要3分钟.丙过河要4分钟，丁过河要5分钟。晓美每次只能赶2只马过河，要把4只马都赶到对岸去.最少要多少分钟?_____
A: 16
B: 17
C: 18
D: 19
参考答案: A
本题解释:参考答案:A
题目详解:两只马可以同时过河(骑一只，赶一只)，若要时间最短.一定要让耗时最长的两只马同时过河;把马赶到对面后要尽量骑耗时最短的马返回。安排如下：先骑甲、乙过河，骑甲返回，共用5分钟;再骑丙、丁过河，骑乙返回，共用8分钟;最后再骑甲、乙过河.用3分钟，故最少要用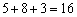

3、单选题  地上放着一个每一面上都有一个数的六面体箱子，对面两个数的和均为27，甲能看到顶面和两个侧面，这三个面上的数字之和是35;乙能看到顶面和另外两个侧面，且这三个面上的数字和为47。箱子贴地一面的数字是_____。
A: 14
B: 13
C: 12
D: 11
参考答案: B
本题解释:正确答案是B考点趣味数学问题解析题目给出对面数字之和为27，则注意将其余条件中出现的对面合在一起。从这一点出发，可以看出若将甲与乙看到的面合在一起，则实际共看到2个顶面与4个不同的侧面。而四个不同侧面恰为两组对面，也即其数字之和为27×2=54，因此顶面的数字为(35+47-54)÷2=14，于是底面数字为27-14=13，故正确答案为B。

4、单选题  从平面A外一点P引与A相交的直线，使得P点与交点的距离等于1，则满足条件的直 线条数一定不可能是：_____
A: 0条
B: 1条
C: 2条
D: 无数条
参考答案: C
本题解释:正确答案是C考点几何问题解析当P点与平面A的垂直距离小于1时，这样的直线有无数条;当P点与平面A的垂直距离等于1时，这样的直线有1条，当P点与平面A的垂直距离大于1时，这样的直线有0条，所以不会出现有2条的情况，正确答案为C。

5、单选题  三位采购员定期去某市场采购，小王每隔9天去一次，大刘每隔6天去一次，老杨每隔7天去一次，三人星期二第一次在这里相会，下次相会将在_____。
A: 星期一
B: 星期五
C: 星期一
D: 星期四
参考答案: C
本题解释:C【解析】此题乍看上去是求9，6，7的最小公倍数的问题，但这里有一个关键词，即“每隔”，“每隔9天”也即“每10天”，所以此题实际上是求10，7，8的最小公倍数。既然该公倍数是7的倍数，那么肯定下次相遇也是星期二。（10，7，8的最小公倍数是5×2×7×4=280，280÷7=40，所以下次相遇肯定还是星期二。）