1、单选题  连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米，则正八面体的体积为_____立方厘米。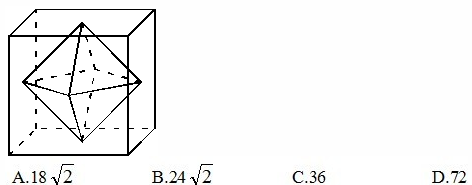A: A
B: B
C: C
D: D
参考答案: C
本题解释:正确答案是C考点几何问题解析

2、单选题  赵先生34岁，钱女士30岁，一天，他们碰上了赵先生的三个邻居，钱女士问起了他们的年龄，赵先生说：他们三人的年龄各不相同，三人的年龄之积是2450，三人的年龄之和是我俩年龄之和。问三个邻居中年龄最大的是多少岁?_____
A: 42
B: 45
C: 49
D: 50
参考答案: C
本题解释:正确答案是C考点年龄问题解析三个人的年龄之积为2450，对2450做因式分解得2450=2×5×5×7×7，三个人的年龄之和为64。所以试着把5个因数组合成3个不同的整数，使他们的和为64。可知5、10、49符合要求，5+10+49=64，故三个邻居中年龄最大是49岁。故正确答案为C。标签构造调整

3、单选题  某通讯公司对3542个上网客户的上网方式进行调查，其中1258个客户使用手机上网，1852个客户使用有线网络上网，932个客户使用无线网络上网。如果使用不只一种上网方式的有352个客户，那么三种上网方式都使用的客户有多少个?_____
A: 148
B: 248
C: 350
D: 500
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析解析1：设三种上网方式都使用的客户有y个，则只使用两种方式上网的有(352-y)个，只使用一种方式上网的有(3542-352)个，根据题意可得：1258+1852+932=(3542-352)+2×(352-y)+3×y，解得y=148，因此三种上网方式都使用的客户有148个，故正确答案为A。解析2：设三种上网方式都使用的客户有y个，则只使用两种方式上网的有(352-y)个，前者重复计算了2次，后者重复计算了1次，根据题意可得：1258+1852+932-2y-(352-y)=3542，解得y=148，此三种上网方式都使用的客户有148个，故正确答案为A。备注：三集合容斥原理中，将只符合一个条件、只符合两个条件和三个条件都符合的分别看作三个整体，以A、B、C表示三个集合，以X、Y、Z分别表示只符合一个条件、只符合两个条件和三个条件都满足的部分，则有A+B+C=X+2Y+3Z及A∪B∪C=X+Y+Z。标签三集合容斥原理公式整体考虑公式应用

4、单选题  一辆汽车在笔直的公路上行驶，两次拐弯后，仍在原来方向上平等前进，那么，这两次拐弯的角度可能是_____。
A: 第一次右拐50度，第二次左拐130度
B: 第一次右拐50度，第二次左拐50度
C: 第一次左拐50度，第二次左拐50度
D: 第一次右拐50度，第二次右拐50度
参考答案: B
本题解释:正确答案是B考点几何问题解析

5、单选题  某单位向希望工程捐款，其中部门领导每人捐50元，普通员工每人捐20元，某部门所有人员共捐款320元。已知该部门部门总人数超过10人，问该部分可能有几名部门领导?_____
A: 1
B: 2
C: 3
D: 4
参考答案: B
本题解释:正确答案是B考点不定方程问题解析假定该部门领导、普通员工分别为X、Y，根据题意可得，50X+20Y=320，X+Y>10。改写上述方程为5X+2Y=32，可知X必为偶数，排除A、C;将其余选项代入验证，若X=2，则Y=11，X+Y=13>10，符合要求;若X=4，则Y=6，X+Y=10，不符合要求。故正确答案为B。