1、单选题  某单位安排职工参加百分制业务知识考试，小周考了88分，还有别外2人的得分比他低。若所有人的得分都是整数，没有人得满分，且任意5人的得分不完全相同，问参加考试的最多有多少人?_____
A: 38
B: 44
C: 50
D: 62
参考答案: C
本题解释:正确答案是C，全站数据:本题共被作答1次，正确率为0.00%，易错项为B解析为了让参加考试的人”最多”，则尽可能在每一个分数段都有尽可能多的人分数相同。从88分-99分，共有12个整数分数可以重复，同时又由于”任意5人的得分不完全相同”，所以要求重复的分数的人数最多为4人。这样一共有48人，再加上两个低于88分的人，所以最多50人。故正确答案为C。速解本题与”抽屉原理”的反客为主思想完全相同，逆向思维简化思维量。考点抽屉原理问题

2、单选题  小明每天必须做家务，做一天可得3元钱，做得特别好时每天可得5元钱，有一个月(30天)他共得100元，这个月他有_____天做得特别好。
A: 2
B: 3
C: 5
D: 7
参考答案: C
本题解释:正确答案是C考点鸡兔同笼问题解析设做得好的天数为n，则有5n+3(30-n)=100，解得n=5，故正确答案为C。

3、单选题  甲乙两地相距20公里，小李、小张两人分别步行和骑车，同时从甲地出发沿同一路线前往乙地，小李速度为4.5公里/小时，小张速度为27公里/小时，出发半小时后，小张返回甲地取东西，并在甲地停留半小时后再次出发前往乙地，问小张追上小李时，两人距离乙地多少公里?_____
A: 8.1
B: 9
C: 11
D: 11.9
参考答案: D
本题解释:正确答案是D考点行程问题解析根据运动过程可知，小张从出发到再次从甲地出发，共用时1.5个小时(出发半小时、返回半小时、甲地停留半小时)。在这段时间内，小李前进了4.5×1.5=6.75公里。此后运动过程即小张对小李的追及过程，追及距离为6.75公里，追及时间为6.75÷(27-4.5)=0.3小时，因此追上时距离乙地20-27×0.3=11.9公里。故正确答案为D。

4、单选题  某机关20人参加百分制的普法考试，及格线为60分，20人的平均成绩为88分，及格率为95%。所有人得分均为整数，且彼此得分不同。问成绩排名第十的人最低考了多少分?_____
A: 88
B: 89
C: 90
D: 91
参考答案: B
本题解释:正确答案是B考点多位数问题解析要使第十名成绩尽可能的低，那么其他人应该尽可能的高，那么前九名应该分别为100、99、98、97、96、95、94、93、92分，而最后一名未及格，最多59分，此十人成绩之和为923，还剩837分。现要把这837分分给其余10个人，而在这10个人成绩排名第十的人成绩最高，要使其得分最低，则这10人的成绩应尽可能接近。易知此10人平均分为83.7，据此可构造79、80、81、82、83、84、85、86、88、89，因此成绩排名第十的人最低考了89分。故正确答案为B。

5、单选题  下图是一个奥林匹克五环标志。这五个环相交成9部分：A、B、C、D、E、F、G、H、I。请将数字1、2、3、4、5、6、7、8、9分别填入这9个部分中，使得五环内的数字之和恰好构成五个连续的自然数。那么，这五个连续自然数的和的最大值是多少?_____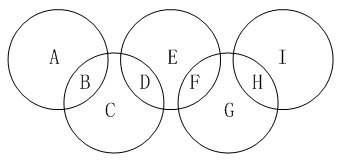A: 65
B: 75
C: 70
D: 102
参考答案: C
本题解释:正确答案是C考点趣味数学问题解析因为B、D、F、H同时出现在两个圆圈中而其他数都出现在一个圆圈中，所以五个圆圈中的总和为1+2+3+……+9+B+D+F+H≤45+9+8+7+6=75。若五个圆圈中的总和为75，则B+D+F+H=9+8+7+6=30，又因为五个环内的数字和恰好构成五个连续的自然数，所以这五个环内的数字只能是13、14、15、16、17，考虑两端两个圆圈中的总和，S=(A+B)+(H+I)≥13+14=27，但B+H≤9+8=17，A+I≤4+5=9，所以S最大为26，与上面的结论矛盾，所以五个圆圈中的总和不可能为75，又因为五个连续自然数的和是5的倍数，所以五个圆圈中的总和最大为70。当(A、B、C、D、E、F、G、H、I)=(9、7、3、4、2、6、1、8、5)时，五个圆圈的总和就可以取到70，故正确答案为C。