1、单选题  甲、乙、丙、丁四人，其中每三个人的岁数之和分别是55、58、62、65。这四个人中年龄最小的是_____。
A: 7岁
B: 10岁
C: 15岁
D: 18岁
参考答案: C
本题解释:正确答案是C考点平均数问题解析将55、58、62、65直接相加，可知其值等于原来四个数之和的3倍，于是可知原四个数字之和为(55+58+62+65)÷3=80，因此最小的数为80-65=15。故正确答案为C。

2、单选题  某公司去年有员工830人，今年男员工人数比去年减少6%，女员工人数比去年增加5%，员工总数比去年增加3人，问今年男员工有多少人?_____
A: 329
B: 350
C: 371
D: 504
参考答案: A
本题解释:正确答案是A考点和差倍比问题解析设去年男员工X人，女员工Y人，由题意知：X+Y=830，5%Y 91EXAM.org-6%X=3，解得X=350。今年男员工减少了，所以人数小于350，只有A符合条件，故正确答案为A。秒杀技由题知，今年男员工数是去年的94%，所以今年男员工数可被94%整除，根据选项，只有A符合。故正确答案为A。标签数字特性

3、单选题  A: 1
B: 1/2007
C: 2007
D: 1/1035
参考答案: B
本题解释:正确答案是B考点数列问题解析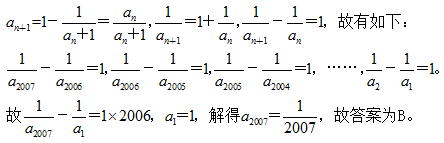

4、单选题  某单位为业务技能大赛获奖职工发放奖金，一、二、三等奖每人奖金分别为800、700和500元。11名获一、二、三等奖的职工共获奖金6700元，问有多少人获得三等奖?_____
A: 3
B: 4
C: 5
D: 6
参考答案: D
本题解释:正确答案是D，全站数据:本题共被作答1次，正确率为100.00%解析假设一、二、三等奖的人数分别是x、y、z，则列方程组800x+700y+500z=6700简化为8x+7y+5z=67••••••①x+y+z=11••••••②此时，题目转化为求解不定方程，无法直接得到结果，但是可以采用消元结合排除法来解决。思路一：倍数关系。消去未知数z，(①-5×②)，得到3x+2y=12，所以y只能取3的倍数。所以y=3，则推出x=2，z=6。故正确答案为D。思路二：排除法。消去无关未知数y，(7×②-①)，得到2z-x=10，此时根据选项代入，z只能取大于5的数，否则x将为负值，所以只能选D选项。秒杀法：按照平均值的思想，如果11个人的平均奖金为600元(只考虑500元和700元的平均值)，那么总奖金应该为6600元，但是由于题目中还包含800元的获奖者，所以只有当获得500元的人超过半数，才能够使总金额达到6700元甚至更低，只能选D。速解本题主要考察的是对于不定方程的处理方式，通过寻找倍数关系或者结合选项利用排除法来解决。但是由于题目类似于十字交叉法和平均值问题的设题方式，也可以通过加权的方式定性思维，结合选项秒杀。考点不定方程问题笔记编辑笔记

5、单选题  某班有70%的学生喜欢打羽毛球，75%的学生喜欢打乒乓球，问喜欢打乒乓球的学生中至少有百分之几喜欢打羽毛球?_____
A: 30%
B: 45%
C: 60%
D: 70%
参考答案: C
本题解释:正确答案是C考点容斥原理问题解析设该班共有100人，则喜欢打羽毛球的有70人，喜欢打乒乓球的有75人;要使喜欢打羽毛球的人中喜欢打乒乓球的最少，那么所有不喜欢打羽毛球的人都喜欢打乒乓球，即100-70=30人，此时喜欢打乒乓球的学生中喜欢打羽毛球的人数为75-30=45人，为最少，45÷75=60%。故正确答案为C。标签赋值思想