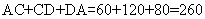1、单选题  (2004广东)两艘渡轮在同一时刻垂直驶离H河的甲、乙两岸相向而行，一艘从甲岸驶向乙岸，另一艘从乙岸开往甲岸，它们在距离较近的甲岸720米处相遇。到达预定地点后，每艘船都要停留10分钟，以便让乘客上船下船，然后返航。这两艘船在距离乙岸400米处又重新相遇。问：该河的宽度是多少?_____
A: 1120米
B: 1280米
C: 1520米
D: 1760米
参考答案: D
本题解释:参考答案
题目详解:如下图所示，设从甲、乙两岸出发的船分别为A船、B船，全程为x米，则：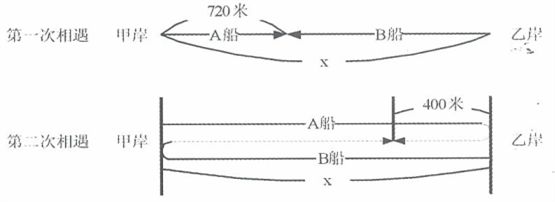

2、单选题  A、B两地相距540千米。甲、乙两车往返行驶于A、B两地之间，都是到达一地之后立即返回，乙车较甲车快。设两辆车同时从A地出发后第一次和第二次相遇都在途中P地。那么两车第三次相遇为止，乙车共走了多少千米?（）
A: 120
B: 1440
C: 2160
D: 2880
参考答案: C
本题解释:参考答案:C
题目详解:根据题意，可知：第一次相遇，甲、乙总共走了2个全程，第二次相遇，甲、乙总共走了4个全程，乙比甲快，相遇又在P点。所以可以推出：从第一次相遇到第二次相遇，甲从第一个P点到第二个P点，路程正好是第一次的路程，则P到A点的路程为P到B点路程的2倍。假设一个全程为3份，第一次相遇甲走了2份，乙走了4份;第二次相遇，乙正好走了1份到B地，又返回走了1份;2个全程里乙走了：(540÷3)×4=180×4=720千米，乙总共走了：720×3=2160千米。所以，选C考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题

3、单选题  某团体从甲地到乙地，甲、乙两地相距100千米，团体中一部分人乘车先行，余下的人步行，先坐车的人到途中某处下车步行，汽车返回接先步行的那部分人，全部人员同时到达。已知步行速度为8千米/小时，汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间?_____
A: 5.5小时
B: 5小时
C: 4.5小时
D: 4小时
参考答案: B
本题解释:参考答案:B
题目详解:根据题意，二队同时出发又同时到达，则二队步行的距离相等，乘车的距离也相等。设第一队乘车的距离是X，则步行的距离是100-X，那么第二队步行的距离也是100-X，汽车从第一队人下车到回来与第二队相遇所行驶的距离(即空车行使的距离)是：100-2×(100-X)=2X-100根据汽车从出发到与第二队相遇所用时间与第二队步行的时间相同，可列方程：[X+(2x-100)]÷40=(100-x)÷8解得，x=75。所用总时间为(以第一队为例)：乘车时间+步行时间=(75÷40)+(100-75)÷8=5小时所以，选B。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线一次相遇问题

4、单选题  甲、乙两人分别从A、B两地同时出发，相向而行，乙的速度是甲的A: 4500米
B: 6500米
C: 7500米
D: 8650米
参考答案: C
本题解释:参考答案:C
题目详解:解法一：设甲的速度为x，则乙的速度为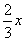B: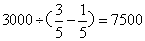

5、单选题  甲、乙两人分别从圆形跑道直径A、B两端同时出发相向而行，在离A地60米的地方相遇，两人继续前进，再一次相遇在离A地80米处。这个圆形跑道的长度为多少?_____
A: 260米
B: 400米
C: 800米
D: 1600米
参考答案: A
本题解释:参考答案:A
题目详解:第一次相遇时，两人走过的距离之和为半个圆周，此时甲走了60米;从第一次相遇到第二次相遇的D点，两人走过的距离之和为一个圆，因此甲又走了120米。因此跑道的总长度为：