1、单选题  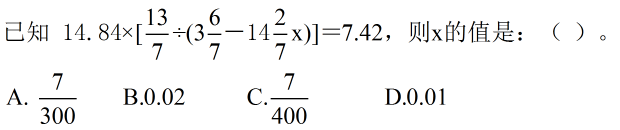_____ A: A
B: B
C: C
D: D
参考答案: D
本题解释:正确答案是D考点计算问题解析

2、单选题  甲、乙、丙、丁四人共同做一批纸盒，甲做的纸盒数是另外三人做的总和的一半，乙做的纸盒数是另外三人做的总和的1/3，丙做的纸盒数是另外三人做的总和的1/4，丁一共做了169个，则甲一共做了_____纸盒。
A: 780个
B: 450个
C: 390个
D: 260个
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析分析题意可知，甲、乙、丙分别做了总纸盒数的1/3、1/4、1/5，那么总的纸盒数为169÷(1-1/3-1/4-1/5)=780个，甲一共做了780×1/3=260个。故正确答案为D。

3、单选题  某地劳动部门租用甲、乙两个教室开展农村实用人才培训。两教室均有5排座位，甲教室每排可坐10人，乙教室每排可坐9人。两教室当月共举办该培训27次，每次培训均座无虚席，当月培训1290人次。问甲教室当月共举办了多少次这项培训?_____
A: 8
B: 10
C: 12
D: 15
参考答案: D
本题解释:正确答案是D考点和差倍比问题解析乙教室可坐9人，可知乙培训过的人数含有因子3，而总的培训人数1290也含有因子3，因此甲教室培训过的人数也必然含有3因子。而甲教室可坐50人，因此要使甲教室培训过的人数也含有3因子，则其举办次数必然含有3因子，因此只有C、D符合。将C选项代入，可知此时乙教室举办过15次培训，其总人数的尾数为5，而甲教室培训的总人数尾数总是为0，因此甲、乙教室的培训人数尾数为5，不符合要求。故正确答案为D。秒杀技由题意，甲教室每次培训50人，乙教室每次培训45，假设甲乙的次数分别为X、Y，则可得50X+45Y=1290，观察等式可知45Y的尾数必然为0，因此Y必然为偶数，从而X为奇数，仅D符合。故正确答案为D。

4、单选题  某班同学要订A、B、C、D四种学习报，每人至少订一种，最多订四种，那么每个同学有多少种不同的订报方式?_____
A: 7种
B: 12种
C: 15种
D: 21种
参考答案: C
本题解释:正确答案是C考点排列组合问题解析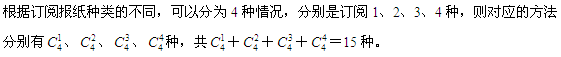

5、单选题  某社区组织开展知识竞赛，有5个家庭成功晋级决赛的抢答环节，抢答环节共5道题。计分方式如下：每个家庭有10分为基础分：若抢答到题目，答对一题得5分，答错一题扣2分;抢答不到题目不得分。那么，一个家庭在抢答环节有可能获得_____种不同的分数。
A: 18
B: 21
C: 25
D: 36
参考答案: B
本题解释:正确答案是B考点排列组合问题解析抢到0题，得分情况：对0题;抢到1题，得分情况：对0题、对1题;抢到2题，等分情况：对0题、对1题、对2题;同理可推知，抢到n题，得分情况有n+1种，而共有5题，所以总得分情况为1+2+3+4+5+6=21种。故正确答案为B。