1、单选题  从一张1952mm×568mm的长方形纸片上，剪下一个边长尽可能大的正方形，如果剩下的部分不是正方形，那么在剩下的纸片上再剪下一个边长尽可能大的正方形。按照上面的过程不断地重复，最后一共可剪得正方形多少个？_____
A: 8
B: 10
C: 12
D: 14
参考答案: D
本题解释:从长1952mm、宽568mm的长方形纸片上首先可剪下边长为568mm的正方形，这样的正方形的个数恰好是1952除以568所得的商，而余数恰好是剩下的长方形的宽，于是有：1952÷568=3…248，568÷248=2…72，248÷72=3…32，72÷32=2…8，32÷8=4，因此一共可得到正方形3+2+3+2+4=14（个），故正确答案为D。

2、单选题  已知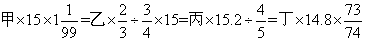A: 甲
B: 乙
C: 丙
D: 丁
参考答案: B
本题解释:参考答案:B
题目详解:原式化简为=

3、单选题  计算：(2+4+6+8+…+2010)-(1+3+5+7+…+2009)=_____。
A: 995
B: 1011
C: 1111
D: 1005
参考答案: D
本题解释:【解析】原式=（2-1）+（4-3）+（6-5）+（8-7）+…+（2010-2009）=1+1+1+1+…+1从2到2010共有1005个偶数,所以原式等于1005个1相加,等于1005,故本题答案为D。

4、单选题  一警官2004年前三个月、后四个月、中间5个月的月平均出警次数分别为46次、36次、54次，问这个警官去年的月平均出警次数为多少次?_____
A: 49
B: 48
C: 46
D: 42
参考答案: C
本题解释:参考答案:C
题目详解:根据题意：前三个月出警次数为：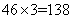

5、单选题  某大型企业的8个车间分布在一条环形铁路旁(如图)。四列货车在铁道上转圈，货车到某一车间时，所需装卸工的人数已在图上标出，装卸工可以固定在车间，也可以随车流动。问：至少需要多少装卸工才能满足装卸要求?_____
A: 235
B: 237
C: 238
D: 239
参考答案: A
本题解释:参考答案:A
题目详解:利用“核心法则”可知，答案直接得到是235人。备注：用户“传说中的疯子”(2010-10-0616:11:00)，认为：题有问题!什么是核心法则，或者又叫焦点规则?但经过分析，我们认为该题没有问题，答案也不存在歧义核心法则如果有M辆车和N(N>M)个工厂，所需装卸工的总数就是需要装卸工人数最多的M个工厂所需的装卸工人数之和。(若M≥N，则把各个点上需要的人加起来即答案)考查点:数量关系>数学运算>统筹问题>人员分配问题