1、单选题  某学校操场的一条环形跑道长400米，甲练习长跑，平均每分钟跑250米;乙练习自行车，平均每分钟行550米，那么两人同时同地同向而行，经过x分钟第一次相遇，若两人同时同地反向而行，经过y分钟第一次相遇，则下列说法正确的是_____。
A: x-y=1
B: y-x=5/6
C: y-x=1
D: x-y=5/6
参考答案: D
本题解释:正确答案是D考点行程问题解析同时同地同向而行有：(550-250)x=400;同时同地反向而行有：(550+250)y=400。联立解得x=4/3，y=1/2，因此x-y=4/3-1/2=5/6，故正确答案为D。

2、单选题  现有甲、乙两个水平相当的技术工人需进行三次技术比赛，规定三局两胜者为胜方。如果在第一次比赛中甲获胜，这时乙最终取胜的可能性有多大?_____。
A: 1/3
B: 1/4
C: 1/2
D: 1/6
参考答案: B
本题解释:正确答案是B考点概率问题解析比赛为三局两胜制，甲先赢一场，故乙赢得比赛，下两场必须都胜利。而甲乙水平相当，故每场赢得比赛的概率都为0.5，则乙最后赢得比赛的概率为0.5×0.5=0.25，即1/4，故正确答案为B。

3、单选题  A: A
B: B
C: C
D: D
参考答案: D
本题解释:正确答案是D考点计算问题解析解析1：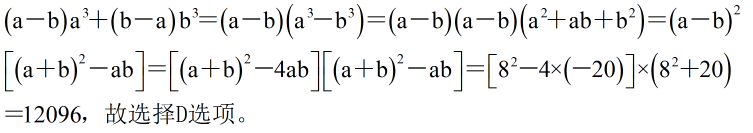

4、单选题  要在一块边长为48米的正方形地里种树苗，已知每横行相距3米，每竖列相距6米，四角各种一棵树，问一共可种多少棵树苗?_____
A: 128棵
B: 132棵
C: 153棵
D: 157棵
参考答案: C
本题解释:正确答案是C考点计数模型问题解析应用单边植树公式，每行种48÷6+1=9棵，每列种48÷3+1=17棵，故一共可种9×17=153棵，正确答案为C。公式：单边线性植树：棵树=总长÷间隔+1。标签公式应用

5、单选题  把一个正四面体的每个表面都分成9个相同的等边三角形，用任意颜色给这些小三角形上色，要求有公共边的小三角形颜色不同，问最多有多少个小三角形颜色相同?_____
A: 15
B: 12
C: 16
D: 18
参考答案: A
本题解释:正确答案是A考点几何问题解析先看一个面上的情况，要是颜色相同的三角形最多，最多有6个(如下图左侧图所示)，此时其他面上能与之颜色相同的三角形最多只能有3个(如下图右侧图所示)。因此颜色相同的三角形最多有6+3×3=15个，正确答案为A。