1、单选题  三位采购员定期去某市场采购，小王每隔9天去一次，大刘每隔6天去一次，老杨每隔7天去一次，三人星期二第一次在这里相会，下次相会将在_____。
A: 星期一
B: 星期五
C: 星期一
D: 星期四
参考答案: C
本题解释:C【解析】此题乍看上去是求9，6，7的最小公倍数的问题，但这里有一个关键词，即“每隔”，“每隔9天”也即“每10天”，所以此题实际上是求10，7，8的最小公倍数。既然该公倍数是7的倍数，那么肯定下次相遇也是星期二。（10，7，8的最小公倍数是5×2×7×4=280，280÷7=40，所以下次相遇肯定还是星期二。）

2、单选题  某单位依据笔试成绩招录员工，应聘者中只有1/4被录取。被录取的应聘者平均分比录取分数线高6分，没有被录取的应聘者平均分比录取分数线低10分，所有应聘者的平均分是73分。问录取分数线是多少分?_____
A: 80
B: 79
C: 78
D: 77
参考答案: B
本题解释:正确答案是B考点平均数问题解析赋值应聘者共4人，一人录取，3人被淘汰。假定录取分数线为A，则可知被录取者的分数为A+6，没有被录取的3个人的平均分为A-10分。则根据题意得，A+6+3(A-10)=4×73，解得A=79。因此正确答案为B。

3、单选题  一条长度为30米、宽度为3米的未划停车位的路边，最差的情况也可以停2米宽、3米长的汽车多少辆?_____
A: 5辆
B: 7辆
C: 8辆
D: l5辆
参考答案: A
本题解释:【解析】分三种情况:第一种:汽车如果与道路垂直。每辆车的车距应尽可能的大，但距离必须小于2米（否则可以再停一辆），当两辆车的车距为2米时，最少可停（30-2）÷（2+2）=7（辆），那么最差的情况下至少可以停8辆车;第二种:汽车如果与道路平行。每辆车的车距应尽可能的大，但距离小于3米，当两辆车的车距为3米时，最少可停（30-3）÷（3+3）=4.5（辆），即停5辆。第三种:汽车与道路有平行与垂直两种情况并存，则停的汽车数量应介于5辆和8辆之间。而题干是问的最差的情况，故最少停5辆车。

4、单选题  某月刊杂志，定价2.5元，劳资处一些人订全年，其余人订半年，共需510元，如果订全年的改订半年，订半年的改订全年，共需300元，劳资处共多少人？_____
A: 20
B: 19
C: 18  
D: 17
参考答案: C
本题解释: 【解析】本题用解方程的方法也可以解答，但是速度较慢。由题意可知，如果劳资处所有人都订一年半的话，总计810元;而单人订一年半的月刊需元;所以共有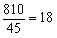

5、单选题  小刚和小强租一条小船，向上游划去，不慎把空塑料水壶掉进江中，当他们发现并掉过头时，水壶与船已经相距2千米，假定小船的速度是每小时4千米，水流速度是每小时2千米，那么他们追上水壶需要多少时间?_____
A: 0.2小时
B: 0.3小时
C: 0.4小时
D: 0.5小时
参考答案: D
本题解释:参考答案:.D
题目详解:此题是水中追及问题，已知路程差是2千米，船在顺水中的速度是船速+水速。水壶漂流的速度只等于水速，所以速度差=船顺水速度-水壶漂流的速度=(船速+水速)-水速=船速。路程差÷船速=追及时间2÷4=0.5(小时)。所以，选D考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题