1、单选题 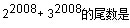 A: 1
B: 3
C: 5
D: 7
参考答案: D
本题解释: 【解析】求尾数的题目，底数留个位，指数除以4留余数（余数为0看为4），比如20683847 就是留底数个位8，3847除以4得数是余3，取3，就变成求8的3次方尾数；因此在这个题目中2008除以4余数为0，取4;所以等于变成2的4次方+3的4次方，尾数是7。

2、单选题  某市居民用电实行分段式收费，以人为单位设定了相同的基准用电度数，家庭人均用电量超过基准用电度数的部分按照基准电费的两倍收取电费。某月，A家庭5口人用电250度，电费175元;B家庭3口人用电320度，电费275元。该市居民每人的基准用电为_____度。
A: 50
B: 35
C: 30
D: 25
参考答案: C
本题解释:正确答案是C考点分段计算问题解析设每人基准用电为m，基准电费为n，则可得方程组如下：n×5m+2n×(250-5m)=175，n×3m+2n×(320-3m)=275，联立解得m=30。故正确答案为C。

3、单选题  (2006北京应届，第3题)若干个同学去划船，他们租了一些船，若每船4人则多5人，若每船5人则船上有4个空位，共有多少个同学?_____
A: 17
B: 19
C: 26
D: 41
参考答案: D
本题解释:参考答案
题目详解:依题意：假设有

4、单选题  小张的手表和闹钟走时都不准，手表比标准时间每9小时快3分钟，闹钟比标准时间每6小时慢5分钟。一天，小张发现手表指示9点27分钟，闹钟刚好指示9点41分，那么至少要经过_____小时，手表和闹钟才能指示同一时刻。
A: 6
B: 9
C: 12
D: 15
参考答案: C
本题解释:正确答案是C考点钟表问题解析

5、单选题  如右图所示，△ABC是等腰直角三角形，AB=12，AD的长度是CD的2倍，四边形EBCD与△AED的面积之比为3：2，AE的长度是_____。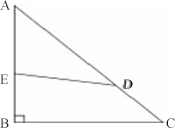A: 6.9
B: 7.1
C: 7.2
D: 7.4
参考答案: C
本题解释:正确答案是C考点几何问题解析四边形EBCD与三角形AED的面积之比为3：2，则三角形ABC与三角形AED的面积之比为5：2。已知AD的长度是CD的2倍，则AD的长度是AC的2/3。作DF垂直AB于点F，则DF=2/3BC(相似三角形原理)，三角形ABC的面积=1/2×AB×BC，三角形AED的面积=1/2×AE×DF=1/2×AE×2/3BC代入之前的比例式，可得AE=3/5AB=36/5=7.2。所以正确答案为C。