1、单选题  某市园林部门计划对市区内30处绿化带进行补栽，每处绿化带补栽方案可从甲、乙两种方案中任选其中一方案进行。甲方案补栽阔叶树80棵，针叶树40株;乙方案补栽阔叶树50株、针叶树90株。现有阔叶树苗2070株、针对树苗1800株，为最大限度利用这批树苗，甲、乙两种方案要应各选_____。
A: 甲方案18个、乙方案12个
B: 甲方案17个、乙方案13个
C: 甲方案20个、乙方案10个
D: 甲方案19个、乙方案11个
参考答案: A
本题解释:正确答案是A考点统筹规划问题解析假定甲方案X个、乙方案Y个，根据题意：X+Y=30，80X+40Y≤2070，50X+90Y≤1800，并使得数字越接近2070和1800越好。可直接将选项代入验证。首选甲方案或乙方案最多的两个极端情况(极端情况很有可能不符合而被排除)，若为C，则80×20+50×10=2100>2070，排除;若为B，则80×17+50×13=1910>1800，排除。若为A，阔叶树用80×18+50×12=2040株，针叶树40×18+90×12=1800株，剩余30株;若为D，阔叶树用80×19+50×11=2070株，针叶树40×19+90×11=1750株，剩余50株。故正确答案为A。

2、单选题  某服装店老板去采购一批商品，其所带的钱如果只买某种进口上衣可买120件，如果只买某种普通上衣则可买180件。现在知道，最后该老板买的进口上衣和普通上衣的数量相同，问他最多可以各买多少件?_____
A: 70件
B: 72件
C: 74件
D: 75件
参考答案: B
本题解释:正确答案是B考点和差倍比问题解析根据题意，设钱数为360元，则进口上衣3元，普通上衣2元，因此可以各买360÷(3+2)=72件。

3、单选题  甲乙丙丁四个数的和为43，甲数的2倍加8，乙数的3倍，丙数的4倍，丁数的5倍减去4，都相等。这四个数各是多少?_____
A: 141289
B: 161296
C: 1110814
D: 141298
参考答案: D
本题解释:正确答案是D考点计算问题解析解法1：设甲数为a，乙数为b，丙数为c，丁数为d，由题意有：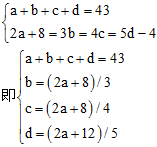

4、单选题 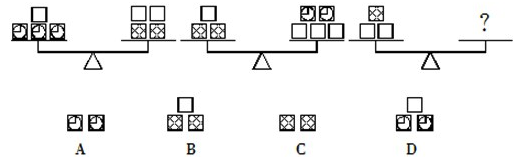 A: A
B: B
C: C
D: D
参考答案: A
本题解释:正确答案是A考点趣味数学问题解析设空白图案为a，交叉图案为b，钟表图案为c，故可得如下：a+c×3=a×2+b×2，a+b×2=c×2+a×3，解得c=3a，b=4a;则可得a×2+b=6a=2c，故正确答案为A。

5、单选题  某大学某班学生总数为32人。在第一次考试中有26人及格，在第二次考试中有24人及格。若两次考试中都没有及格的有4人，那么两次考试都及格的人数是_____。
A: 22
B: 18
C: 28
D: 26
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析由题意，两次考试中至少有一次及格的人数为32-4=28(人)，设两次考试都及格的人数是n，则有：28=26﹢24-n，解得n=22。故正确答案为A。注：两集合容斥原理公式为A∪B=A+B-A∩B。标签两集合容斥原理公式