1、单选题  蜘蛛有8条腿，蜻蜓有6条腿和2对翅膀，蝉有6条腿和1对翅膀，现在这三种小虫共18只，有118条腿和18对翅膀，蜘蛛，蜻蜓，蝉各几只_____
A: 5、5、8 
B: 5、5、7 
C: 6、7、5 
D: 7、5、6
参考答案: A
本题解释:【答案】A。解析：这是道复杂的“鸡兔同笼”问题，首先，蜻蜓和蝉都是6条腿，数腿的时候可以放在一起考虑，因此蜘蛛有（118—6×18）÷（8—6）=5只，因此蜻蜓和蝉共有18—5=13只，从而蜻蜓有（18—1×13）÷（2—1）=5只，蝉有13—5=8只。

2、单选题  四年级有4个班，不算甲班其余三个班的总人数是131人;不算丁班其余三个班的总人数是134人;乙、丙两班的总人数比甲、丁两班的总人数少1人，问这四个班共有多少人?_____
A: 177
B: 178
C: 264
D: 265
参考答案: A
本题解释:正确答案是A考点和差倍比问题解析解析1：设甲、乙、丙和丁四个班的人数分别为a、b、c和d，根据题意可得，b+c+d=131，a+b+c=134，b+c-(a+d)=-1，联立解得：a+d=89，b+c=88，因此四个班总人数为：89+88=177，故选择A选项。解析2：因为乙、丙两班总人数比甲、乙两班总人数少1人，因此乙、丙两班总人数的3倍就等于(131+134-1)即为264人，乙、丙两班共有：264÷3=88(人)，因此四个班总人数为：88+88+1=177，故选择A选项。秒杀技由“乙、丙两班总人数比甲、乙两班总人数少1人”可知四个班总人数一定为奇数，观察到只有A和D选项符合，而通过题意可知四个班总人数一定小于：131+134=265，故只有A选项符合。标签直接代入数字特性

3、单选题  十几个小朋友围成一圈，按顺时针方向一圈一圈地循环报数。如果报1和报100的是同一人，那么共有多少个小朋友?_____
A: 10
B: 11
C: 13
D: 15
参考答案: B
本题解释:参考答案:B
题目详解:代入法，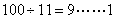

4、单选题  小红把平时节省下来的全部五分硬币先围成一个正三角形，正好用完，后来又改围成一个正方形，也正好用完。如果正方形的每条边比三角形的每条边少用5枚硬币，则小红所有五分硬币的总价值是_____。
A: 1元         
B: 2元     
C: 3元        
D: 4元
参考答案: C
本题解释:C。【解析】设三角形每条边X，正方形为Y，那么Y=X-5，同时由于硬币个数相同，那么3X=4Y，如此可以算出X=20，则硬币共有3×20=60个，硬币为5分硬币，那么总价值是5×60=300（分），得出结果。

5、单选题  从平面A外一点P引与A相交的直线，使得P点与交点的距离等于1，则满足条件的直线条数一定不可能是：_____
A: 0条
B: 1条
C: 2条
D: 无数条
参考答案: C
本题解释:正确答案是C考点几何问题解析当P点与平面A的垂直距离小于1时，这样的直线有无数条;当P点与平面A的垂直距离等于1时，这样的直线有1条，当P点与平面A的垂直距离大于1时，这样的直线有0条，所以不会出现有2条的情况，正确答案为C。