1、单选题  一个自然数，被7除余2，被8除余3，被9除余1，1000以内一共有多少个这样的自然数?_____
A: 5
B: 2
C: 3
D: 4
参考答案: B
本题解释:参考答案:B
题目详解:7、8的最小公倍数为56，根据"差同减差，公倍数做周期"可知：所有满足条件的数可表示为56n-5，也就是除以56余5;要让所有56n-5中满足被9除余1：最小数是n=3时：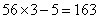

2、单选题  袋子里有一百多个小球，五个五个取出来剩余4个，六个六个取出来剩余3个，八个八个取出来剩余1个，问袋子里面有多少个小球?_____
A: 109
B: 119
C: 129
D: 139
参考答案: C
本题解释:参考答案:C
题目详解:设小球共有

3、单选题  把几百个苹果平均分成若干份，每份9个余8个，每份8个余7个，每份7个余6个。这堆苹果共有多少个?_____
A: 111
B: 143
C: 251
D: 503
参考答案: D
本题解释:参考答案:D
题目详解:此题为剩余定理中差同的情况，根据"差同减差，最小公倍数做周期"可知：即苹果数加上一个，就是7、8和9的公倍数;而7、8和9的最小公倍数是504，正好在几百的范围内：因此这堆苹果有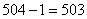

4、单选题  有一盒乒乓球，每次8个8个的数，10个10个的数，12个12个的数，最后总是剩下3个。但是9个9个数，刚好数完，问这盒乒乓球至少有多少个?_____
A: 144
B: 180
C: 243
D: 324
参考答案: C
本题解释:参考答案:C
题目详解:每次8个8个的数，10个10个的数，12个12个的数，最后总是剩下3个，因此此题是余数问题中余同的情况。即根据"余同取余，最小公倍数做周期"可知：8、10、12的最小公倍数120，只需要用3加上最小公倍数，直至能够被9整除为止;容易得到，

5、单选题  一个数列为1，-1，2，-2，-1，1，-2，2，1，-1，2，-2…………则该数列的第2009项为_____
A: -2
B: -1
C: 1
D: 2
参考答案: C
本题解释:参考答案:C
题目详解:观察数列可知：该数列每8项为一组，为1，-1，2，-2，-1，1，-2，2，;而后不断循环;要求出第2009项数值，必须知道2009项在这一组中位于第几位：即200÷8=251…………1，即2009在第252组中位于第一位，即为1;所以，选C。考查点:数量关系>数学运算>计算问题之数的性质>余数问题>一个被除数，多个除数>基本形式>中国剩余定理