1、单选题  _____ A: A
B: B
C: C
D: D
参考答案: D
本题解释:正确答案是D考点几何问题解析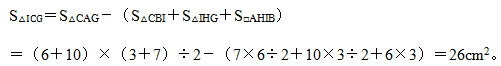

2、单选题  建造一个容积为8立方米，深为2米的长方体无盖水池。如果池底和池壁的造价分别为120元/平米和80元/平米，那么水池的最低总造价是_____元。
A: 1560
B: 1660
C: 1760
D: 1860
参考答案: C
本题解释:正确答案是C考点几何问题解析本题考查几何等量最值性质。容积为8，深为2，则底面积为4，当底面为正方形时，周长最小，此时造价最低，故正方形边长为2，则底面周长为2×4=8，而侧面面积=深度×底面周长=2×8=16，则总造价=120×4+80×16=1760。故正确答案为C。标签几何等量最值性质

3、单选题  某单位举办庆国庆茶话会，买来4箱同样重的苹果，从每箱取出24千克后，结果各箱所剩的苹果重量的和，恰好等于原来一箱的重量。那么原来每箱苹果重多少千克?_____
A: 16
B: 24
C: 32
D: 36
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析解析1：设原来每箱苹果重x千克，根据题意可得：4(x-24)=x，解得x=32，故选择C选项。解析2：原来一共4箱苹果，由“从每箱取出24千克后，结果各箱所剩的苹果重量的和，恰好等于原来一箱的重量”，可知总共取出来的苹果重量是原来3箱苹果的重量，因此原来每箱苹果的重量为：24×4÷3=32，故选择C选项。

4、单选题  如下图所示，梯形ABCD，AD∥BC，DE⊥BC，现在假设AD、BC的长度都减少10%，DE的长度增加10%，则新梯形的面积与原梯形的面积相比，会怎样变化?_____ 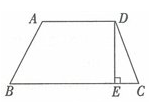A: 不变
B: 减少1%
C: 增加10%
D: 减少10%
参考答案: B
本题解释:正确答案是B考点几何问题解析

5、单选题  报社将一定的奖金分发给征文活动获奖者，其中一等奖学金是二等的2倍，二等奖学金是三等的1.5倍，如果一、二、三等奖学各评选两人，那么一等奖获得者将得2400元奖金;如果一等奖只评选一人，二、三等奖各评选两人，那么一等奖的奖金是_____。
A: 2800元
B: 3000元
C: 3300元
D: 4500元
参考答案: C
本题解释:正确答案是C考点和差倍比问题解析设三等奖学金为X，则二等奖学金为1.5X，一等奖学金为3X=2400，X=800，总奖金=2(X+1.5X+3X)=8800，现在令三等奖学金为Y，有3Y+2(Y+1.5Y)=8800，得Y=1100，则一等奖学金为3300。故正确答案为C。