1、单选题  一个长方体形状的盒子长、宽、高分别为20厘米、8厘米和2厘米，现在要用一张纸将其六个面完全包裹起来，要求从纸上剪下的部分不得用作贴补，请问这张纸的大小可能是下列哪一个?_____
A: 长25厘米，宽17厘米
B: 长26厘米，宽14厘米
C: 长24厘米，宽21厘米
D: 长24厘米，宽14厘米
参考答案: C
本题解释:正确答案是C考点几何问题解析由题意知，盒子的表面为：2×(20×8+20×2+2×8)=432(平方厘米)，纸的面积必须比盒子的表面积大才能完全包裹盒子。计算四个选项中长和宽相乘产生的面积值，A项为25×17=425(平方厘米)，B项为26×14=364(平方厘米)，C项为24×21>480>432(平方厘米)，D项为24×14<26×14=364(平方厘米)，仅C项的面积值大于432。故正确答案为C。

2、单选题  31.21×16＋3.121×120﹢312.1×6.2的值是_____。
A: 3121
B: 2808.9
C: 4125
D: 3768
参考答案: B
本题解释:正确答案是B解析原式＝31.21×（16＋12＋62）＝31.21×90＝312.1×9，观察式子可知，结果是小数，故正确答案为B。计算问题

3、单选题  一名外国游客到北京旅游，他要么上午出去游玩，下午在旅馆休息，要么上午休息，下午出去游玩，而下雨天他只能一天都待在屋里。期间，不下雨的天数是12天，他上午待在旅馆的天数为8天，下午待在旅馆的天数为12天，他在北京共待了多少天?_____
A: 16天
B: 20天
C: 22天
D: 24天
参考答案: A
本题解释:正确答案是A考点容斥原理问题解析解析1：设这个人在北京共待了n天，其中12天不下雨，那么n-12天下雨。由两集合容斥原理公式得：上午待在旅馆的天数+下午待在旅馆的天数-上下午都待在旅馆的天数(就是下雨的天数)=总天数-上下午都不待在旅馆的天数(根据题意不存在这样的一天)。即：8+12-(n-12)=n-0，解得n=16。故正确答案为A。解析2：设游客在京期间下雨天数为x。因为他上午待在旅馆的8天中包括两部分：因下雨无法出去的天数(x)和因下午出去游玩而休息的天数(8-x);同理，下午待在旅馆的12天中包括两个部分：因下雨无法出去的天数(x)和因上午出去游玩而休息的天数(12-x)。由题意可得：(8-x)+(12-x)=12，解得x=4，所以一共在北京待了16天。故正确答案为A。

4、单选题  下图中的甲和乙都是正方形，BE=6厘米，EF=4厘米。那么，阴影部分ABC的面积是多少平方厘米?_____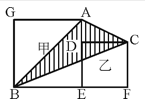A: 20
B: 24
C: 21
D: 18
参考答案: D
本题解释:正确答案是D考点几何问题解析

5、单选题  从一副完整的扑克牌中，至少抽出_____张牌，才能保证至少6张牌的花色相同。
A: 21
B: 22
C: 23
D: 24
参考答案: C
本题解释:正确答案是C考点抽屉原理问题解析一副完整的扑克牌有54张，转变思维，考虑54张牌已经在手中，尽量不满足6张牌花色相同的前提下，最多可以发出几张牌。此时显然是先把每种花色发5张，外加大王、小王，共计22张牌，尚未满足要求，但任意再发出1张就满足要求了，故最多可以发出23张牌，因此至少要发出23张牌才能保证至少6张牌的花色相同，正确答案为C。