1、单选题  6辆汽车排成一列纵队，要求甲车和乙车均不在队头或队尾，且正好间隔两辆车。问共有多少种不同的排法?_____
A: 48
B: 72
C: 90
D: 120
参考答案: A
本题解释:正确答案是A，全站数据:本题共被作答1次，正确率为100.00%解析假设六辆车的位置为A-B-C-D-E-F，按照题干的说法，甲乙均不在首位，即不能放在A或F，同时中间还需要间隔两辆车，所以甲乙的位置只能选择B或E。即题目转化为”四辆汽车放入ACDF位置，甲乙两车放入BE位置，一共有多少种方法?”按照排列组合的解法，前四辆汽车一共有P44=24种情况，甲乙两车一共有P22=4种情况，所以两者相乘，一共有48种情况。故正确答案为A。速解本题需要辅助画图理解，得到关键信息”甲乙只能在B或E位置”，即可求解。本题如果增加一个车位，就非常复杂了，需要分类讨论。而在现有情况下，不需要分类讨论。考点排列组合问题笔记编辑笔记

2、单选题  李明从图书馆借来一批图书，他先给了甲5本和剩下的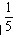A: 30 
B: 40 
C: 50 
D: 60
参考答案: A
本题解释: 【解析】A。解法一、设李明共借书x本，则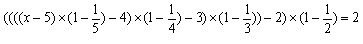

3、单选题  有一筐苹果，把它们三等分后还剩2个苹果;取出其中两份，将它们三等分后还剩两个：然后再取出其中两份，又将这两份三等分后还剩2个。问：这筐苹果至少有几个_____
A: 19
B: 23
C: 24
D: 26
参考答案: B
本题解释:参考答案:B
题目详解:根据中国剩余定理：我们面对着最后剩下的2个苹果，它们是把某两份苹果三等分后剩下的;换句话说，把所剩的2个苹果与三等分的三份苹果放在一起，应是上一轮分割中的两份;所以这个总数必须能被2整除。题中又问这筐苹果"至少"有几个：从而上述总数又应尽可能地少，三份苹果中，每份最少有1个苹果，于是三份便是3个。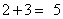

4、单选题  已知2008被一些自然数去除，得到的余数都是10，那么，这些自然数共有_____。
A: 10
B: 11
C: 12
D: 9
参考答案: B
本题解释:【答案解析】解析：余10=>说明2008-10=1998都能被这些数整除。同时，1998=2×3×3×3×37，所以，取1个数有37，2，3。---3个。，只取2个数乘积有3×37，2×37，3×3，2×3。---4个。，只取3个数乘积有3×3×37，2×3×37，3×3×3，2×3×3。---4个。只取4个数乘积有3×3×3×37，2×3×3×37，2×3×3×3。---3个。只取5个数乘积有2×3×3×3×37---1个。总共3+4+4+3+1=15，但根据余数小于除数的原理，余数为10，因此所有能除2008且余10的数，都应大于10=>2，3,3×3，2×3被排除。综上，总共有3+4+4+3+1-4=11个。

5、单选题  一张考试卷共有10道题，后面的每一道题的分值都比前面一道题多2分。如果这张考卷的满分为100分，那么第8道题的分值应为多少?_____
A: 14
B: 15
C: 16
D: 17
参考答案: B
本题解释:正确答案是B考点数列问题解析10道题的分值是公差为2的等差数列。设第一道题的分值为y，则第10道题的分值为y+2×(10-1)=y+18。由题意得(y+y+18)×10÷2=100，解得y=1，则第8道题的分值为1+2×(8-1)=15分，故正确答案为B。