1、单选题  (2005广东下，第11题)要在一块边长为48米的正方形地里种树苗，已知每行相距3米，每竖列相距6米，四角各种一棵树，问一共可种多少棵树苗?_____
A: 128棵
B: 132棵
C: 153棵
D: 157棵
参考答案: C
本题解释:参考答案:C
题目详解:根据“每横行相距3米”、“四角各种一棵树”可知，应使用不封闭植树理论，且为两端均植树问题。两端均植树：点数=总长÷间距+1确定总长：48确定间距：3带入公式：点数=总长÷间距+1=48÷3+1=17根据“每竖列相距6米”，“四角各种一棵树”可知，应使用不封闭植树理论，且为两端均植树问题。两端均植树：点数=总长÷间距+1确定总长：48确定间距：6带入公式：点数=总长÷间距+1=48÷6+1=9总可种树：17×9=153棵。因此，选C。考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均植树

2、单选题  有一个周长为300米的封闭花坛，每3米挖坑栽树，挖了30个后，接到通知，以后改为每5米挖坑栽树，请问还需要挖多少个坑?_____
A: 40
B: 42
C: 43
D: 45
参考答案: B
本题解释:参考答案:B
题目详解:“在一个周长为300米的封闭花坛”，可知是只有一端植树问题。挖了30个坑，实际上是29个3米间距，即已经挖了的距离是：3×29=87米，剩下的距离是：300-29×3=213米。每5米挖一个坑，带入只有一端植树问题的公式：棵数=总长÷间距=213÷5=42…3因此42个坑还多出3米所以，选B。考查点:数量关系>数学运算>特殊情境问题>植树问题>只有一端植树

3、单选题  某人要上某大厦的10楼，他从1楼到5楼用了100秒，按此速度，他到10楼还需要的时间为_____秒。
A: 225
B: 125
C: 100
D: 150
参考答案: B
本题解释:参考答案:B
题目详解:从1楼到5楼共有5-1=4段楼梯，每层楼梯花了100÷4=25秒。从5楼到10楼共有10-5=5段楼梯，从5楼道10楼需要时间为：25×5=125秒。考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均植树

4、单选题  如下图所示，街道ABC在B处拐弯，在街道一侧等距装路灯，要求A、B、C处各装一盏路灯，这条街道最少装多少盏路灯?_____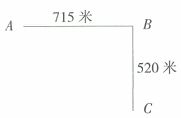A: 18
B: 19
C: 20
D: 21
参考答案: C
本题解释:参考答案:C
题目详解:根据题意，要求的是最少装灯的数量且路等间距相等，可知A--B和B--C间路灯的间距得相等;所以要求先715和520的最大公约数，715=5×11×13，

5、单选题  王杰要在一个长50米，宽30米的长方形水池旁植树，每隔10米植1棵，并且四个角都植树。一共可以植_____棵。
A: 14
B: 15
C: 16
D: 17
参考答案: C
本题解释:参考答案:C
题目详解:根据题意，可知此题为封闭的只有一端植树问题。确定总长为长方形的周长：(50+30)×2=160(米);确定间距：10带入只有一端植树问题的公式：棵数=总长÷间距=160÷10=16(棵)。考查点:数量关系>数学运算>特殊情境问题>植树问题>只有一端植树