1、单选题  在前100个自然数中，能被3除尽的数相加，所得到的和是多少?_____
A: 1250
B: 1683
C: 1275
D: 1400
参考答案: B
本题解释:参考答案:B本题得分:
题目详解:根据题意，在前100中，能被3除尽的数，即个位数字之和为3的倍数;“在前100个自然数中，能被3整除的数”有3、6、9、12、15、18……故可以转化为首项为3，末项为99，公差为3，共有33项的等差数列;在前100个自然数中，能被3除尽的数的和——等差数列求和：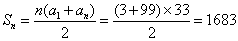

2、单选题  在865后面补上三个数字，组成一个六位数，使它能分别被3、4、5整除，且使这个数值尽可能的小，这个数是_____
A: 865010
B: 865020
C: 865000
D: 865230
参考答案: B
本题解释:参考答案:B本题得分:
题目详解:能被5整除的数：末尾数字是0或5，四个选项都符合;能被4整除的数：末尾两位数可被4整除，排除A、D项;能被3整除的数：各位数字之和可被3整除，排除C;所以，选B。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除特征

3、单选题  一个三位自然数正好等于它各位数字之和的18倍，则这个三位自然数是_____。
A: 999
B: 476
C: 387
D: 162
参考答案: D
本题解释:参考答案:D本题得分:
题目详解:根据题意，这个三位数是18的倍数，则它一定能被9和2整除：被9整除的数：各位数字之和能被9整除，排除B;能被2整除的数：末位数为0、2、4、6、8，排除A、C;所以，选D。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除特征

4、单选题  商店里有六箱货物，分别重15、16、18、19、20、31千克，两个顾客买走了其中五箱，已知一个顾客买的货物重量是另一个顾客的2倍。商店剩下的一箱货物重多少千克_____。
A: 16
B: 18
C: 19
D: 20
参考答案: D
本题解释:参考答案:D本题得分:
题目详解:6箱货物总重为：15+16+18+19+20=119千克;已知一个顾客买的货物重量是另一个顾客的2倍，那么说明这五箱货物的总重能被3整除：已知119÷3=39……2，所以减掉的一箱重量应该是除以3余数为2，15÷3=516÷3=5……118÷3=619÷3=6……120÷3=6……231÷3=10……1因此，只有20的符合题目，所以剩下的一箱是20kg;所以，选D。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除的性质

5、单选题  修剪果树枝干，第1天由第1位园丁先修剪1棵，再修剪剩下的1/10，第2天由第2位园丁先修剪2棵，在修剪剩下的1/10，……，第N天由第N位园丁先修剪N棵，结果N天就完成了，问如果每个园丁修剪的棵数相等，共修剪了_____果树。
A: 46棵
B: 51棵
C: 75棵
D: 81棵
参考答案: D
本题解释:参考答案:D本题得分:
题目详解:“第N天由第N位园丁先修剪N棵，结果N天就完成”，说明第N位园丁修剪了N棵，而每位园丁修剪的棵数相等，故果树一共有