1、单选题  一个班有50名学生，他们的名字都是由2个或3个字组成的。将他们平均分为两组之后，两组的学生名字字数之差为10。此时两组学生中名字字数为2的学生数量之差为_____。
A: 5
B: 8
C: 10
D: 12
参考答案: C
本题解释:【解析】C。不定方程问题。由题意两组学生名字字数相差10，两边人数相同，即其中一组比另一组三名字人数多10人，则2名字人数少10人。

2、单选题  一个商家要将自己的广告牌装在一条马路的一边，计划每隔4米装一块广告牌。在该马路上，每隔7米都栽种一棵树。已知这段马路长1092米，且一端是树，请问在不砍掉树的情况下，这段马路上可以装_____块广告牌。
A: 234
B: 233
C: 157
D: 156
参考答案: A
本题解释:【答案】A。解析：方法一：如果没有树的话，马路应该可以装1092÷4+1=274（块）广告牌。但因为马路上原来栽有树木，则每隔4×7=28（米）处是树和广告牌重合的地方，不能立广告牌，只需求得广告牌与树木重合之处共有多少，减去即可。至此，本题转化成求在1092米的道路上，间隔28米，可栽种多少树木的问题。套入公式，该条道路上间隔28米处可以种树的棵数1092÷28+1=40。因此，这段马路上能装的广告牌的数量为：274—40=234（块）。方法二：题目可以看做是周期问题。每隔28米可装广告牌数量为28÷4+1=8（块），其中两端都种有树，则28米内可以装广告牌8—2=6（块）。1092米内间隔为28米的路段共有1092÷28=39（个），所以共可装广告牌的数量为6×39=234（块）。

3、单选题  红领巾春节慰问小组在确定去敬老院演出的节目单时，遇到如下问题：除夕夜的演出有唱歌、舞蹈、杂技、小品4个节目。如果要求唱歌不排在第4项，舞蹈不排在第3项，杂技不排在第2项，小品不排在第1项，那么，满足上述要求的节目单，共有多少种不同的排法?_____
A: 7 
B: 9 
C: 15 
D: 18
参考答案: B
本题解释:B【解析】 采用穷举法。满足上述要求的节目单共有以下九种不同的排法：（1）唱、小、杂、舞;（2）唱、舞、杂、小;（3）唱、舞、小、杂;（4）舞、小、唱、杂;（5）舞、唱、杂、小;（6）舞、唱、小、杂;（7）杂、小、唱、舞;（8）杂、唱、小、舞;（9）杂、舞、唱、小。故本题正确答案为B。

4、单选题  地上放着一个每一面上都有一个数的六面体箱子，对面两个数的和均为27。甲能看到顶面和两个侧面，这三个面上的数字之和是35;乙能看到顶面和另外两个侧面，且这三个面上的数字和为47。箱子贴地一面的数字是：_____
A: 14
B: 13
C: 12
D: 11
参考答案: B
本题解释:参考答案:B
题目详解:先求出顶面的数字：甲、乙二人看到的数加起来一共为：2组对面加上2倍的顶面数字;则顶面的数字为：(35+47-27×2)÷2=14;根据对面两个数的和均为27：底面的数字为：

5、单选题   甲、乙两种含金样品熔成合金，如甲的重量是乙的一半，得到含金68%的合金;如甲的重量是乙的3.5倍，得到含金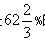A: 72% 
B: 64% 
C: 60% 
D: 56%
参考答案: A
本题解释:【解析】A。解析：设甲的含金百分数为x，乙的含金百分数为y，可列方程x+2y=（1+2）×68%,3.5x+y=（1+3.5）×