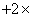1、单选题  甲、乙、丙、丁四人做纸花，已知甲、乙、丙三人平均每人做了37朵，乙、丙、丁三人平均每人做了39朵，已知丁做了41朵，问甲做了多少朵?_____
A: 35朵
B: 36朵
C: 37朵
D: 38朵
参考答案: A
本题解释:正确答案是A考点平均数问题解析由“甲、乙、丙三人平均每人做了37朵”和“丁做了41朵”可知四人一共做了：37×3+41=152，又知“乙、丙、丁三人平均每人做了39朵”，所以甲做了：152-39×3=35朵，故正确答案为A。

2、单选题  甲、乙、丙三名运动员囊括了全部比赛项目的前三名，他们的总分分别是8、7和17分，甲得了一个第一名，已知各个比赛项目分数相同，且第一名的得分不低于二、三名得分的和，那么比赛共有多少个项目?_____
A: 3
B: 4
C: 5
D: 6
参考答案: B
本题解释:【答案解析】全部比赛前三名的总分为8+7+17=32分，每个项目前三名的分数和至少是3+2+1=6分，所以每个项目前三名的分数和应该是32的大于6的约数，只能是8、16、32;如果是16或32，因为甲得了一个第一，所以甲的得分应大于8，不合题意，所以每个项目前三名的分数和是8分，共有项目32÷8=4个。

3、单选题  Ａ、Ｂ、Ｃ三本书，至少读过其中一本的有20人，读过A书的有10人，读过B书的有12人，读过C书的有15人，读过A、B两书的有8人，读过B、C两书的有9人，读过A、C两书的有7人。三本书全读过的有多少人?_____
A: 5
B: 7
C: 9
D: 无法计算
参考答案: B
本题解释:B【解析】根据题目的不同可以挑选其中的任意2组或者3组公式答题。首先这里不考虑都不参与的元素（1）A+B+T=总人数（2）A+2B+3T=至少包含1种的总人数（3）B+3T=至少包含2种的总人数这里介绍一下A、B、T分别是什么A=x+y+z; B=a+b+c;T=三种都会或者都参加的人数看这个题目我们要求的是看三本书全部读过的是多少人?实际上是求T根据公式：（1） A+B+T=20（2） A+2B+3T=10+12+15=37（3） B+3T=8+9+7=24（2）-（1）=B+2T=17结合（3）得到T=24-17=7人。

4、单选题  某校人数是一个三位数，平均每个班级36人，若将全校人数的百位数与十位数对调，则全校人数比实际少180人，那么全校人数最多可以达到多少人?_____
A: 900
B: 936
C: 972
D: 990
参考答案: C
本题解释:参考答案:C
题目详解:使百位数与十位数对调后，比实际少180人：百位比十位必须大2;根据题意应是九百七十几;又因为这个三位数是36倍数：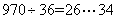

5、单选题  实验小学举办学生书法展，学校的橱窗里展出了每个年级学生的书法作品，其中有28幅不是五年级的，有24幅不是六年级的，五、六年级参展的书法作品共有20幅。一、二年级参展的作品总数比三、四年级参展的作品总数少4幅。一、二年级参展的书法作品共有多少幅?_____
A: 6
B: 10
C: 16
D: 20
参考答案: A
本题解释:参考答案:A
题目详解:28幅不是五年级的，也就是六年级+其他年级=28幅;24幅不是六年级的，也就是五年级+其他年级=24幅;上述两个式子相加得：(五年级+六年级)