1、单选题  6辆汽车排成一列纵队，要求甲车和乙车均不在队头或队尾，且正好间隔两辆车。问共有多少种不同的排法?_____
A: 48
B: 72
C: 90
D: 120
参考答案: A
本题解释:正确答案是A，全站数据:本题共被作答1次，正确率为100.00%解析假设六辆车的位置为A-B-C-D-E-F，按照题干的说法，甲乙均不在首位，即不能放在A或F，同时中间还需要间隔两辆车，所以甲乙的位置只能选择B或E。即题目转化为”四辆汽车放入ACDF位置，甲乙两车放入BE位置，一共有多少种方法?”按照排列组合的解法，前四辆汽车一共有P44=24种情况，甲乙两车一共有P22=4种情况，所以两者相乘，一共有48种情况。故正确答案为A。速解本题需要辅助画图理解，得到关键信息”甲乙只能在B或E位置”，即可求解。本题如果增加一个车位，就非常复杂了，需要分类讨论。而在现有情况下，不需要分类讨论。考点排列组合问题笔记编辑笔记

2、单选题  下图是一个奥林匹克五环标志。这五个环相交成9部分：A、B、C、D、E、F、G、H、I。请将数字1、2、3、4、5、6、7、8、9分别填入这9个部分中，使得五环内的数字之和恰好构成五个连续的自然数。那么，这五个连续自然数的和的最大值是多少?_____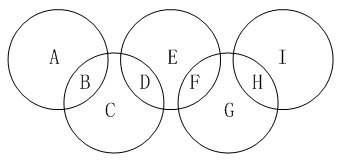A: 65
B: 75
C: 70
D: 102
参考答案: C
本题解释:正确答案是C考点趣味数学问题解析因为B、D、F、H同时出现在两个圆圈中而其他数都出现在一个圆圈中，所以五个圆圈中的总和为1+2+3+……+9+B+D+F+H≤45+9+8+7+6=75。若五个圆圈中的总和为75，则B+D+F+H=9+8+7+6=30，又因为五个环内的数字和恰好构成五个连续的自然数，所以这五个环内的数字只能是13、14、15、16、17，考虑两端两个圆圈中的总和，S=(A+B)+(H+I)≥13+14=27，但B+H≤9+8=17，A+I≤4+5=9，所以S最大为26，与上面的结论矛盾，所以五个圆圈中的总和不可能为75，又因为五个连续自然数的和是5的倍数，所以五个圆圈中的总和最大为70。当(A、B、C、D、E、F、G、H、I)=(9、7、3、4、2、6、1、8、5)时，五个圆圈的总和就可以取到70，故正确答案为C。

3、单选题  完成某项工程，甲单独工作需要18小时，乙需要24小时，丙需要30小时。现按甲、乙、丙的顺序轮班工作，每人工作一小时换班。当工程完工时，乙总共干了多少小时?_____
A: 8小时
B: 7小时44分
C: 7小时
D: 6小时48分
参考答案: B
本题解释:正确答案是B考点工程问题解析解析1：设工程总量为360，则甲乙丙的工作效率分别为20、15、12，三人每小时工作总量为47。由题意可知三人轮班即为循环周期问题，用360除以47商7余数为31，甲乙丙轮班每人7小时后，乙继续工作的工作量为31-20=11。所以最终乙总共干了：7小时+11/15×60分=7小时44分，故正确答案为B。解析2：设工程总量为360，则甲乙丙的工作效率分别为20、15、12，甲每小时比乙多干5，乙每小时比丙多干3，因此乙工作时间必定小于24/3=8小时。观察选项有6小时、7小时和8小时，可选7为参考点，甲乙丙轮班每人工作7小时共完成：(20+15+12)×7=329<360，因此乙工作时间在7小时和8小时之间，故正确答案为B。

4、单选题  某单位招待所有若干间房间，现在安排一支考察队的队员住宿，若每间住3人则有2人无房可住;若每间住4人，则有一间房间不空也不满，则该招待所的房间最多有_____。
A: 4间
B: 5间
C: 6间
D: 7间
参考答案: B
本题解释:正确答案是B考点盈亏问题解析解析1：设房间数为x，则总人数为3x+2，由题意可得：x-1&lt;(3x+2)/4<X，解得2<X<6，因此X最大为5。故正确答案为B。<p>解析2：由"若每间住4人，则有一间房间不空也不满"可知，不空不满的房间住1-3人。设房间数为x，则总人数为3x+2，由题意可得：4(x-1)+1≤3x+2≤4(x-1)+3，解得3≤x≤5，因此x最大为5。故正确答案为B。

5、单选题  如图，街道XYZ在Y处拐弯，XY=1125米，YZ=855米，在街道一侧等距装路灯，要求X，Y，Z处各装一盏路灯，这条街道最少要安装多少盏路灯?_____A: 9月18日
B: 10月14日
C: 11月14日
D: 12月18日
参考答案: C
本题解释:正确答案是C考点周期问题解析A、B、C、D四人的周期分别为6、12、18、30，因此周期的最小公倍数为180。从5月18日向后数180天，180天约为6个月，因此该时间必然落在11月，故正确答案为C。