这段文字意在说明（  ）

A．人才是创新的一部分

B．人才是创新的特点

C．人才是创新的关键

D．人才是创新的原因

14．【解析】C。文段为“总分”结构，首句提出观点：人才是创新的根基，创新驱动实质是人才驱动。后文为解释说明部分，文段首句为中心句，结合选项，C项正确。A选项“一部分”程度过轻且表述不明确；B项“特点”无中生有；D项“原因”无中生有。因此C项当选。

15．中国经济发展进入新常态，最重要的是两个转变，一是经济增速从高速增长转向中高速增长，二是经济发展方式从规模速度型粗放增长转向质量效率型集约增长。第一个转变已接近完成，但第二个转变明显滞后，质量效率型集约增长模式尚未完全形成。我国发展过程中出现的不平衡不协调不可持续问题，与两个转变不同步有很大关系。延续中国经济发展奇迹，必须加快经济发展方式转变，推动经济从高速增长转向高效增长、实现由大到强的质的飞跃。

对这段文字理解有误的是（  ）

A．我国不少地方仍存在经济规模速度型粗放增长现象

B．两个转变同步进行可减少我国经济发展的一些问题

C．新常态推动我国经济发展实现由大到强的质的飞跃

D．我国经济增速已经完成从高速增长转向中高速增长

15．【解析】D。本题为细节判断题，文段与选项一一对应。A项可由“经济发展方式从规模速度型粗放增长转向质量效率型集约增长”“明显滞后”得出；B、C两项对应尾句内容，此三者均与原文相符。D项“已经”一词与文段表达的时态不一致，原文是“已接近完成”说明还未完成。本文为选非题目，所以D项与原文不一致。选择D项。

第二部分  数量关系

（共15题，参考时限15分钟）

一、数字推理。给出一个数列，缺少其中一项，要求你仔细观察数列的排列规律，从四个选项中，选择最合适的一项，使之符合原数列的排列规律。

16． -1，3，-3，5，-5，7，（  ）

A．7           B．8            C．-7             D．-8

16．【解析】C。观察发现数列奇数项分别为：-1、-3、-5、（）为连续负的奇数列，下一项应为-7。选择C项。

17． 13，26，39，52，（  ）

A．55          B．65          C．75             D．85

17．【解析】B。数列变化幅度较小，优先考虑做差。相邻两项做差后均得13，故下一项应为52+13=65。因此选择B项。

18．1，2，3，10，39，（  ）

A．157       B．257        C．390           D．490

18．【解析】D。数列变化幅度较大，幂次无规律，从后向前推发现，39=10×3+3²，10=3×2+2²，3=2×1+1²，即a_n=a_n-1×a_n-2+（a_n-2）²——第三项=前两项的乘积+第一项的平方。因此下一项为39×10+10²=490。D项当选。

19．12.7，20.9，31.1，43.3，（  ）

A．55.5       B．57.5       C．57.7         D．59.7

19．【解析】B。由题意可判断数列为小数数列，简单观察后无规律可循，但数列整体呈现递增趋势，且变化幅度较小，考虑作差，得到新数列为8.2、10.2、12.2、（  ），为公差是2的等差数列，可判断括号内数值为14.2，则题目所求为43.3+14.2=57.5。因此选择B项。

20．

A．55        B．103        C．199        D．212

20．【解析】D。由题意可判断为九宫格数列，寻找每行或者每列相同的规律，可发现9²－17×2=47、4²－26×2=－36。即每行中，第一个数的平方减去第三个数的2倍等于第二个数，则题目所求为15²－2×6.5=212。

二、数学运算。通过运算，选择最合适的一项。

21．甲乙丙三人参加一项测试，三人的平均分为80，甲乙两人的平均分为75，乙丙两人的平均分为80，那么甲丙两人的平均分为（  ）

A．70          B．75           C．80           D．85

21．【解析】D。方法一：根据已知条件三人的平均分为80，甲、乙平均分为75，乙丙平均分为80可得，甲+乙+丙=80×3=240，由甲+乙=75×2=150，则丙=90；由乙+丙=80×2=160，则甲=80；甲+丙=170。所以，甲丙两人的平均分为170÷2=85分。

方法二：甲+丙=2（甲+乙+丙）-（甲+乙）-（乙+丙）=2×80×3-75×2-80×2=170；所以，甲丙两人的平均分为170÷2=85分。选择D项。

22．一批零件若交由赵师傅单独加工，需要10天完成；若交由孙师傅单独加工，需要15天完成。两位师傅一起加工这批零件，需要（  ）天完成

A．5           B．6           C．7            D．8

22．【解析】B。已知完成工程的时间，赋值给工作总量。设工程总量为30，则赵师傅的效率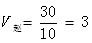 ，孙师傅的效率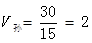，因此两位师傅合作需要30÷（3+2）=6（天）。

23．两辆汽车同时从两地相向开出，甲车每小时行驶60千米，乙车每小时行驶48千米，两车在离两地中点48千米处相遇。则两地相距（  ）千米

A．192       B．224         C．416        D．864

23．【解析】D。两车同时出发到相遇，所走的时间相同，所以路程比等于速度比，。当两车相遇时，距离两地中点48千米，即相遇时，甲比乙多走了48×2=96千米。因为S_甲∶S_乙=5∶4，甲走了5份，乙走了4份，全程是9份，甲比乙多走的1份，对应的是96千米，故两地相距96×9=864千米。因此选择D项。

24．修建一条铁路，如果每4米铺设5根枕木，共需5000根；如果每5米铺设6根枕木，一共要用（  ）根

A．3600 B．4200          C．4800     D．7500

24．【解析】C。由题意可得铁路长度为5000÷5×4=4000（米），则若每5米铺设6根则需要枕木4000÷5×6=4800（根）。因此选择C项。

25．某单位2014年年终评比中，良好等级的人数占总人数3/5。2015年年终评比又多了60人被评为良好等级，此时该等级的人数占总人数9/11。如果在这两年间该单位的人员没有变化，则该单位共有（  ）人。

A．120         B．275       C．330     D．800

25．【解析】B。由题意可设2014年良好等级的人数为3x，则总人数为5x，可得，解方程可得x=55，总人数为5×55=275（人）。

秒杀技：由题意可知总人数必然是11和5的倍数，则可排除A、D，将B项代入满足条件。

26．某服装店有一批衬衣共76件，分别卖给了33位顾客，每位顾客最多买了3件。衬衣定价为100元，买1件按原 价，买2件总价打九折，买3件总价打八折。最后卖完这批衬衣共收入6460元，则买了3件的顾客有（  ）位。

A．4           B．8            C．14             D．15

26．【解析】 C。由题意可设买了1件、2件、3件衣服的人数分别为x、y、z人，则可得x+y+z=33，x+2y+3z=76，100x+200×0.9×y+300×0.8×z=6460，联立求解可得x=4，y=15，z=14。因此选择C项。

27．园林工人用一辆汽车将20棵行道树运往1公里的地方开始种植。在1公里处种第一棵，以后往更远处每隔50米种一棵，该辆汽车每次最多能运三棵树。当园林工人完成任务时，这辆汽车行程最短是（  ）米。

A．20800     B．20900        C．21000          D．21100

27．【解析】C。由题意可得，要汽车行驶距离最短，需要汽车从最远开始运，每次都运3棵。共20棵树，汽车每次最多运3棵，所以共需往返20÷3=6次余2棵，即往返7次，从第七次最远的第20棵树看，单程需行驶1000+（20-1）×50=1950米，第六次种第17棵树，单程需行驶1000+（17-1）×50=1800米，以后每次种树路程减少150米，到第一次种2棵树，单程需行驶1000+50=1050米，再计算往返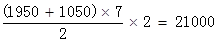（米）。

28．小王早上看到挂钟显示8点多，急忙赶往公司上班。但是到了公司却发现时间和自己出门看到的挂钟时