微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
的比例上升最快的行业是( )。
A.工业 B.建筑业
C.交通业 D.商饮业
94. 从上表数据可以看出,在非农劳动力中,2000 年从事商饮行业的比重约是 1990 年的多少倍?( )
A.2.53倍 B.1.75倍
C.1.45倍 D.0.97倍
95. 根据上表所列数据,下列说法错误的是( )。
A.乡村人口总人口比重不断下降
B.乡村人口中农业劳动力的比重不断下降
C.从事非农劳动的乡村人口不断上升
D.在非农劳动人口中,从事工业、建筑、交通、商饮行业的比例都有不同程度的上升
根据下列图表。回答96~100题。
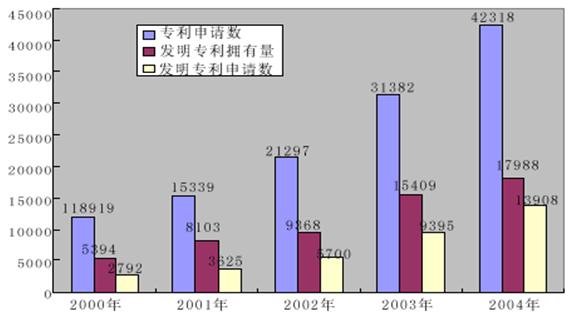
2000—2004年我国大中型企业专利申请及拥有量统计图(单位:件)
2004 年我国部分省、市大中型工业企业专利申请及拥有量统计表 单位:件
|
地区 |
专利申请量(件) |
发明专利申请量(件) |
发明专利拥有量(件) |
|
北京 |
1377 |
544 |
987 |
|
天津 |
2977 |
2540 |
632 |
|
上海 |
3879 |
1611 |
705 |
|
浙江 |
4078 |
1049 |
1953 |
|
江苏 |
3078 |
972 |
1639 |
|
黑龙江 |
643 |
185 |
468 |
|
山东 |
4084 |
933 |
1543 |
|
广东 |
6338 |
3286
|
3254 |
|
四川 |
1050 |
311 |
655 |
|
陕西 |
363 |
120 |
189 |
|
青海 |
44 |
14 |
29 |
96. 2000年至 2004年,我国大中型工业企业发明专利申请数占专利申请数比重最大的年份是( )。
A.2001年 B.2002年 C.2003年 D.2004年
97. 根据上表,2004年我国大中型工业企业发明专利申请量占专利申请量比重最高的地区是( )。
A.北京 B.天津 C.上海 D.广东
98. 根据上图,2000年至2004年间,我国大中型工业企业三项专利统计指标的平均增幅最大的一项是( )。
A.专利申请数 B.发明专利申请数
C.发明专利拥有量 D.三项统计指标之和
99. 根据以上统计信息,下列关于我国大中型工业企业专利情况的表述,错误的一项是( )。
A.2001至2004年间,我国发明专利申请数占专利申请数的比重逐年增加
B.2001至2004年间,我国发明专利拥有量的年均增幅达到了30%
C.2004年,粤、鲁、苏、浙、沪等五地发明专利拥有量之和超过了全国总量的50%
D.根据2001至2004年发明专利拥有量的增长趋势,预计2005年,我国发明专利拥有量将突破20000件。
100. 根据以上统计信息,下列关于大中型工业企业专利状况的表述,正确的一项是( )。
A.2004年,广东省专利申请量为北京的6.2倍、江苏的3.2倍
B.2004年,广东省发明专利拥有量为2939件,占全国的23.0%
C.2004年,广东省发明专利申请量和发明专利申请占专利申请总数的比重都居全国首位
D.2004 年,广东省发明专利申请量占专利申请量的比重为38.3%,超出全国平均水平 5.4个百分点
[申论真题]
一、数字推理
1.C 【解析】分数数列,分数数列最重要的特点就是分子分母可以通分约分。通过分数约分或通分,可将原数列转化为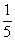 ,
,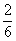 ,
,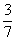 ,
,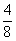 ,分子、分母均为公差为1的等差数列,故接下来的一项为
,分子、分母均为公差为1的等差数列,故接下来的一项为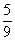 ,即C项
,即C项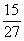 。
。
2.C 【解析】此题为三级特殊数列。首先相邻两项两两做差得:23,24,26,29,34,42;
再对这个数列相邻两项两两做差得:1,2,3,5,8;这是一个典型的递推和数列:1+2=3,2+3=5,3+5=8,5+8=13;故空缺项应为170+(42+13)=225,正确答案为C项。
3.B 【解析】这个数列的共同点就是每项都能被3整除,答案中只有270也能被3整除,所以这道题的正确答案为B项。
4.A 【解析】此题为变指数幂数列,突破点在于32,81,64,25这些特殊数字:1=16,32=25,81=34,64=43,25=52,所以接下来的空缺项应为61=6。
5.D 【解析】此题为前两项相加等于第四项的递推和数列,即:1+2=3,2+2=4,2+3=5,所以接下来的3+4=7,故选择D项。
二、数学运算
6.B 【解析】此题考查的是基本运算能力。根据等差数列的和公式Sn=(a1+an)×n÷2即可得出答案。设题目中最大的偶数为x,则最小的偶数就是x-(24-1)×2,则(x+x-23×2) ×24÷2=1992,解得x=106,故应选B项。
7.A 【解析】此题考查的是对利润的理解:单个商品利润=售价-成本。设定价为y,成本为x,则按定价80%出售,仍获得20%利润,用数学公式表示就是0.8y-x=0.2x,即售价-成本=利润。因此,得y=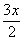 。若按原价出售,则利润为y-x=
。若按原价出售,则利润为y-x=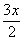 -x=
-x=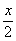 ,即利润率为50%,故应选A项。
,即利润率为50%,故应选A项。
8.A 【解析】根据题意可得,甲,乙,丙,丁的1%分别为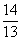 ,
,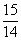 ,
,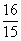 ,
,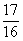 ,这个数列是递减数列,因此甲最大。故应选A项。
,这个数列是递减数列,因此甲最大。故应选A项。
9. D 【解析】此题考查的是相对速度的概念:设甲速率为x,乙速率为y。若两人方向相反,则两人相对速度为x+y,若两人方向相同,则两人相对速度为|x-y|。因为甲、乙从A地,丙从B地同时出发,相向而行,所以甲丙相对速度为(50+35=85)米/分钟,乙丙相对速度为(40+35=75)米/分钟,所以答案必须能整除85和75,因此得到1275,故应选D项。
10.D 【解析】此题是一道典型的利润问题。关键在于明白利润的含义以及打折的含义:多个商品利润=单个商品利润×商品个数,设总共有10件商品,每件成本为10元,按期望获得50%的利润来定价即售价为15元,按15元每售出7件商品。剩下的3件商品按15x出售,则获得利润为(15x-10)×3,则总实际利润为5×7+(15x-10)×3,而期望总利润为10×5=50,所以由这样所获得全部利润,是原来所期望利润的80%,得5×7+(15x-10)×3=50×0.80,得x=0.8,故应选D项。
11. A 【解析】这种题目是典型的集合问题。这个俱乐部一共有69+58-30+12=109人,其中
减去30是因为用会下象棋的和会下围棋的人相加时,多加了次两种象棋都会下的人,故A项为正确答案。
12. C 【解析】植树相关问题。300米的圆形花坛边等距离栽树,每隔5米栽一棵树,意味着要挖坑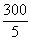 =60个坑,而先前按照每隔3米挖一个坑,挖了30个坑,从第1个坑到第30个坑距离为87米,因此我们看一下已经挖的这些坑中哪些可以被我们所利用,若这些坑能被我们用,则它距离第一个坑的距离就能被15所整除,0-87之间能被15整除的数字有6个,包括(0,15,30,45,60,75),所以还应该挖坑60-6=54个,故应选择C项。
=60个坑,而先前按照每隔3米挖一个坑,挖了30个坑,从第1个坑到第30个坑距离为87米,因此我们看一下已经挖的这些坑中哪些可以被我们所利用,若这些坑能被我们用,则它距离第一个坑的距离就能被15所整除,0-87之间能被15整除的数字有6个,包括(0,15,30,45,60,75),所以还应该挖坑60-6=54个,故应选择C项。
13.C 【解析】此题目为典型的分段计费问题,分段问题就要分段计算。设每月标准电量为x度,超出标准的电量为(100-x)度,则由题意标准电量所产生的电费为0.6x,而超出标准电量部分的电量单价为0.6×0.8=0.48元/度,因此所产生的电费为0.48×(100-x),所以0.6x+0.48×(100-x)=57.6,解此方程,得x=80,故正确答案为C项。 [公共基础知识真题]
14.B 【解析】这属于工程类问题,我们一般用完成任务的百分比来解决此类问题。设一台抽水机x分钟能抽干满水的水池,进水管y分钟能充满水池,则抽水机每分钟抽出蓄水池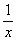 的水,进水管每分钟输入
的水,进水管每分钟输入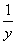 的水。设水池中积水为z,注意:抽水管排水管同时开着。根据题意可得:
的水。设水池中积水为z,注意:抽水管排水管同时开着。根据题意可得:
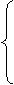 (
(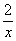 -
-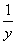 )×40=z ①
)×40=z ①
(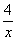 -
-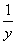 )×16=z ②
)×16=z ②
②-①,得(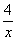 -
-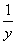 )×16-(
)×16-(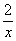 -
-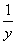 )×40=0,得
)×40=0,得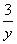 =
=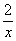 ,代入①式中,得z=
,代入①式中,得z=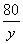 ,用10分钟将水排完意味着(
,用10分钟将水排完意味着(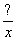 -
-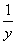 )×10=
)×10=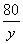 ,即(
,即(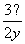 -
-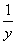 )×10=
)×10=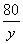 ,解得?=6,故选择B项。
,解得?=6,故选择B项。
15.B 【解析】这是浓度问题,浓度问题的关键就是浓度公式:盐的浓度=
设浓度为3%溶液为100克,加入水的质量为x克,则含有盐的质量为100× 3%=3克,再加入质量为x的水,则溶液质量为(100+x)克,而因为盐的质量并没有改变,所以溶液的浓度为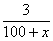 =2%,得50克,所以当第三次加入同样多的水的时候,溶液的质量为100+50+50=200克,而且盐的质量仍然没有改变,所以浓度为
=2%,得50克,所以当第三次加入同样多的水的时候,溶液的质量为100+50+50=200克,而且盐的质量仍然没有改变,所以浓度为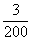 ×100%=1.5%,故选择B项。
×100%=1.5%,故选择B项。
第二部分言语理解与表达
一、选词填空
16. C 【解析】此题主要考查的是词语的搭配以及感情色彩。A项“平衡”不能与“增长势头”搭配,排除;文段中对“投资过快”持反对态度,而B项“保持”是对其肯定,排除; C项与D项都有反对投资增长过快的意思,但相比较而言,“遏制”除了含有“阻止”的意思之外,在感情色彩上还有对不良行为的坚决抵制的意思,故C项为正确答案。
17.D 【解析】“保障”不能与“兴趣”和“义务”搭配,只能是“培养兴趣”和“履行义务”,故选项B、C两项排除;“权力”是指政治上的强制力,而“权利”是指公民或法人依法行政的权力和享受的利益,根据语境,应该选择“权利”。
18.D 【解析】此题考查的主要是连词的运用,对于此类题目最常用的解析方法为将各个答案代入原句中结合语感及语境分析得出准确答案,具体分析如下:A项“既然”和B项“虽然”不能与后半句的连接词“也”搭配,故排除;后半句强调“能力不能脱离知识”,前半句是强调“知识不能离开能力”,二者是并列关系,故应该选表示并列关系的连接词,故正确答案为D项。
19.A 【解析】根据语境,所要填的词与后面的“能力”相呼应,并且语句顺畅,故C、D两项排除;A、B两项读音相同,词形相近,但是词义有区别