微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
2015年全国硕士研究生入学统一考试数学二试题
一、选择题:1~8小题,每小题4分,共32分.下列每题给出的四个选项中,只有一个选项符合
题目要求的,请将所选项前的字母填在答题纸指定位置上.
(1)下列反常积分中收敛的是()
(A)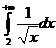 (B)
(B)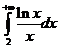 (C)
(C)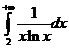 (D)
(D)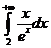
(2)函数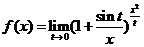 在
在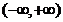 内()
内()
(A)连续 (B)有可去间断点 (C)有跳跃间断点 (D)有无穷间断点
(3)设函数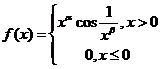
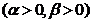 ,若
,若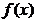 在
在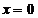 处连续,则()
处连续,则()
(A)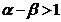 (B)
(B)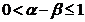 (C)
(C)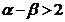 (D)
(D)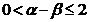
(4) 设函数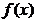 在
在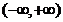 连续,其二阶导函数
连续,其二阶导函数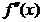 的图形如右图所示,则曲线
的图形如右图所示,则曲线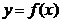 的拐点个数为()
的拐点个数为()
(A)0 (B)1 (C)2 (D)3
(5).设函数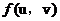 满足
满足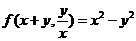 ,则
,则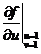 与
与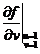 依次是()
依次是()
(A)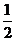 ,0 (B)0,
,0 (B)0,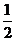 (C)-
(C)-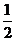 ,0 (D)0 ,-
,0 (D)0 ,-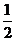
(6). 设D是第一象限中曲线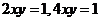 与直线
与直线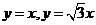 围成的平面区域,函数
围成的平面区域,函数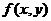 在D上连续,则
在D上连续,则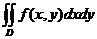 =()
=()
(A) (B)
(B)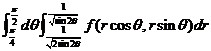
(C) (D)
(D)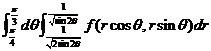
(7).设矩阵A=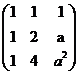 ,b=
,b=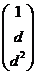 ,若集合Ω=
,若集合Ω=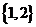 ,则线性方程组
,则线性方程组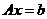 有无穷多个解的充分必要条件为()
有无穷多个解的充分必要条件为()
(A)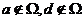 (B)
(B)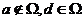 (C)
(C)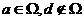 (D)
(D) 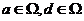
(8)设二次型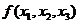 在正交变换
在正交变换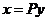 下的标准形为
下的标准形为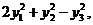 其中
其中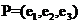 ,若
,若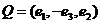 ,则
,则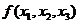 在正交变换
在正交变换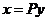 下的标准形为( )
下的标准形为( )
(A):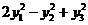 (B)
(B) 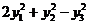 (C)
(C) 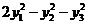 (D)
(D) 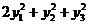
二、填空题:9~14小题,每小题4分,共24分.请将答案写在答题纸指定位置上.
(9) 设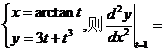
(10)函数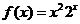 在
在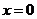 处的n 阶导数
处的n 阶导数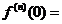
(11)设函数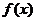 连续,
连续,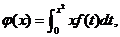 若
若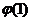
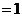 ,
,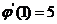 ,则
,则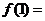
(12)设函数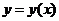 是微分方程
是微分方程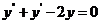 的解,且在
的解,且在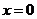 处
处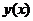 取值3,则
取值3,则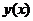 =
=
(13)若函数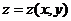 由方程
由方程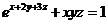 确定,则
确定,则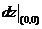 =
=
(14)设3阶矩阵A的特征值为2,-2,1,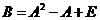 ,其中E为3阶单位矩阵,则行列式
,其中E为3阶单位矩阵,则行列式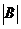 =
=
三、解答题:15~23小题,共94分.请将解答写在答题纸指定位置上.解答应写出文字说明、证明过程或演算步骤.
15、(本题满分10分)
设函数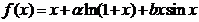 ,
,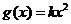 ,若
,若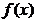 与
与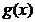 在
在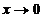 是等价无穷小,求
是等价无穷小,求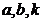 的值。
的值。
16、(本题满分10分)
设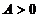 ,D是由曲线段
,D是由曲线段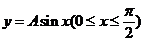 及直线
及直线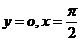 所形成的平面区域,
所形成的平面区域,  ,
,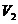 分别表示D绕X轴与绕Y轴旋转所成旋转体的体积,若
分别表示D绕X轴与绕Y轴旋转所成旋转体的体积,若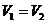 ,求A的值。
,求A的值。
17、(本题满分10分)
已知函数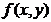 满足
满足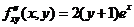 ,
,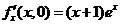 ,
,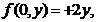 求
求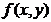 的极值。
的极值。
18、(本题满分10分)
计算二重积分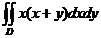 ,其中
,其中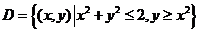 。
。
19、(本题满分10分)
已知函数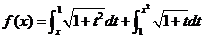 ,求
,求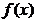 零点的个数。
零点的个数。
20、(本题满分11分)
已知高温物体置于低温介质中,任一时刻物体温度对时间的关系的变化与该时刻物体和介质的温差成正比,现将一初始温度为120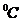 的物体在20
的物体在20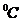 恒温介质中冷却,30min后该物体温度降至30
恒温介质中冷却,30min后该物体温度降至30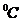 ,若要使物体的温度继续降至21
,若要使物体的温度继续降至21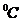 ,还需冷却多长时间?
,还需冷却多长时间?
21、(本题满分11分)
已知函数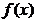 在区间
在区间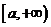 上具有2阶导数,
上具有2阶导数,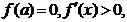 设
设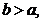 曲线
曲线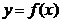 在点
在点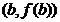 处的切线与X轴的交点是
处的切线与X轴的交点是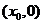 ,证明:
,证明: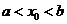 。
。
22、(本题满分11分)
设矩阵 ,且
,且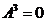 ,(1)求a的值;(2)若矩阵X满足
,(1)求a的值;(2)若矩阵X满足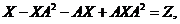 其中
其中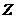 为3阶单位矩阵,求X。
为3阶单位矩阵,求X。
23、(本题满分11分)
设矩阵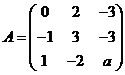 ,相似于矩阵
,相似于矩阵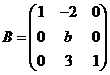 ,
,
(1)求a,b的值(2)求可逆矩阵P,使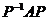 为对角矩阵。
为对角矩阵。
2015年考研数学二真题答案(完整版)
(1)选D
(A)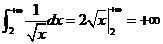 ,发散
,发散
(B)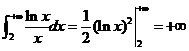 ,发散
,发散
(C)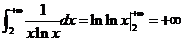 ,发散
,发散
(D)当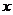 足够大时,
足够大时,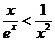 ,
,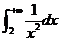 收敛,
收敛,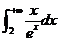 收敛
收敛
(2)选B
当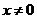 时,
时,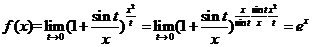
(3)选A
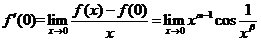 存在
存在
所以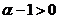 ,且
,且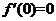
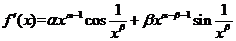
由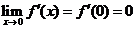 ,得
,得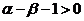 ,
,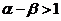
(4)选C
由图易知,拐点为原点和与x正半轴的交点,所以拐点数为2
(5)选D
法一: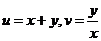
所以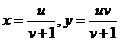
所以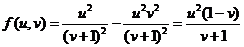
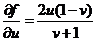 ,
,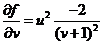
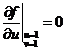 ,
,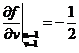
法二: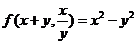 (1)
(1)
(1)式对x求导得,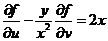 (2)
(2)
(1)式对y求导得,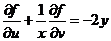 (3)
(3)
由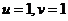 ,得
,得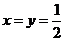 ,代入(2)(3)
,代入(2)(3)
解得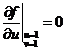 ,
,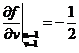
(6)选B
由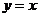 得,
得,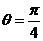
由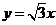 得,
得,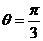
由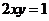 得,
得,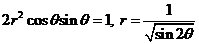
由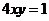 得,
得,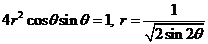
所以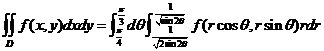
(7)解析:
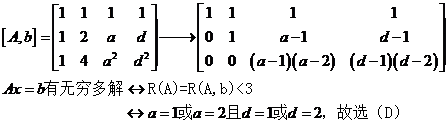
(8)
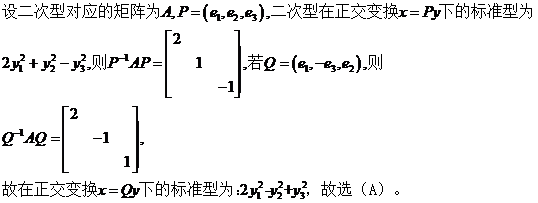
(9)答案: .
.
解: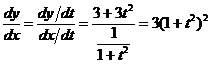 ,
,
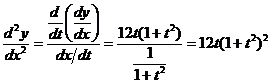 ,
,
因此,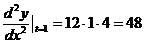 .
.
(10)答案: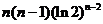 .
.
解: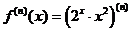
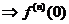
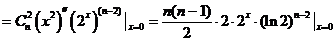
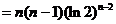 .
.
11.
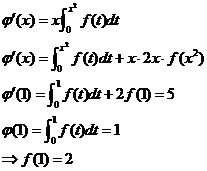
12.
通解是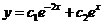
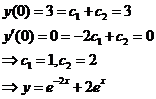
13.
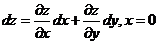
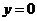
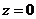
两边对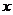 求导
求导
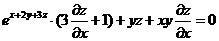
代入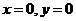
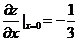
两边对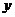 求导
求导
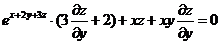
代入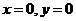
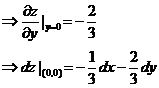
(14)
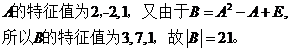
(15)
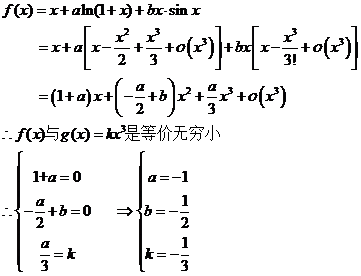
16.解:
由题意得:
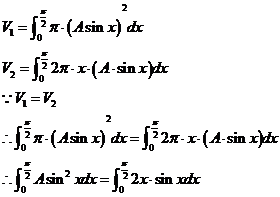
得
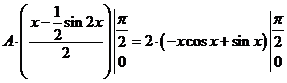
得: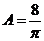
(17)已知函数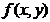 满足
满足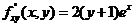 ,
,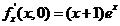 ,
,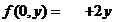 ,求
,求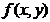 的极值。题干缺条件,无正解。
的极值。题干缺条件,无正解。
18. 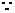
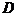 关于
关于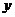 轴对称,
轴对称,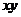 关于
关于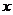 为奇函数,
为奇函数,
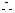
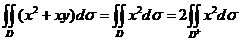 (
(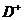 为
为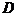 在第1象限的部分)
在第1象限的部分)
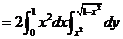
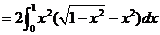

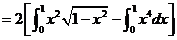
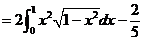
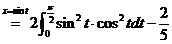
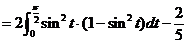
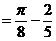 .
.
19.解:
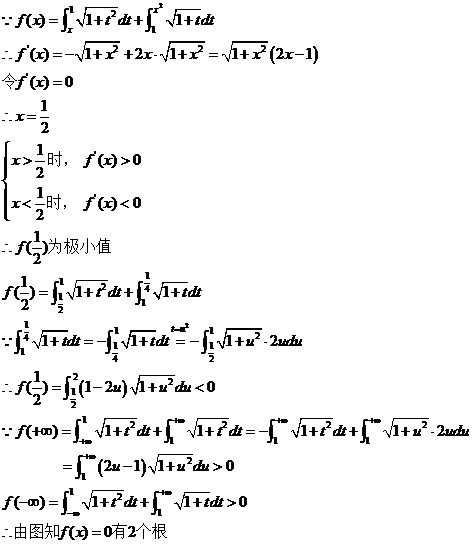
20.解:令物体在t时刻温度为f(t),
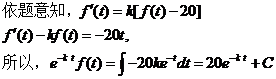
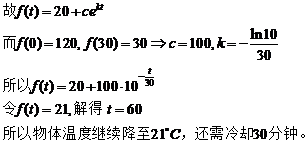
(21)
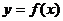 在
在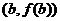 处的切线方程为:
处的切线方程为: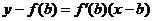
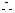 交点
交点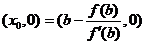
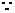
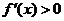 ,
,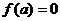
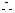
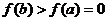 ,即
,即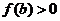
又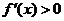
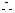
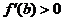 ,
,
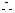
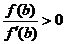
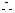
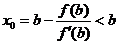 .
.
下证: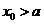 ,即证明:
,即证明: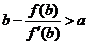 成立.
成立.
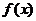 在
在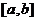 上二阶可导,
上二阶可导,
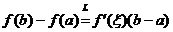
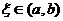
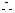
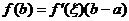 .
.
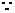
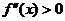 ,
,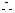
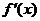 单调递增,
单调递增,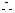
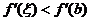
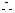
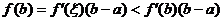 ,
,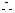
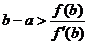 ,
,
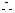
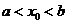 .
.
22
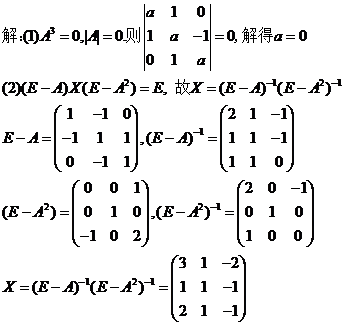
23.