微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
2014年考研数学二真题
一、选择题 1—8小题.每小题4分,共32分.
1.当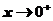 时,若
时,若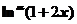 ,
,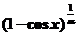 均是比
均是比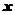 高阶的无穷小,则
高阶的无穷小,则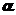 的可能取值范围是( )
的可能取值范围是( )
(A)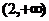 (B)
(B)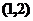 (C)
(C)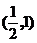 (D)
(D)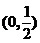
2.下列曲线有渐近线的是
(A)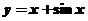 (B)
(B)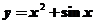 (C)
(C)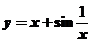 (D)
(D)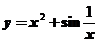
3.设函数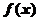 具有二阶导数,
具有二阶导数,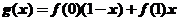 ,则在
,则在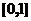 上( )
上( )
(A)当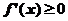 时,
时,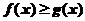 (B)当
(B)当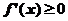 时,
时,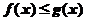
(C)当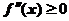 时,
时,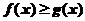 (D)当
(D)当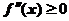 时,
时,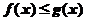
4.曲线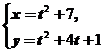 上对应于
上对应于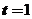 的点处的曲率半径是( )
的点处的曲率半径是( )
(A)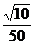 (B)
(B)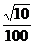 (C)
(C)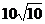 (D)
(D)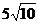
5.设函数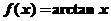 ,若
,若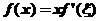 ,则
,则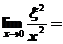 ( )
( )
(A)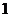 (B)
(B)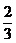 (C)
(C)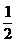 (D)
(D)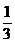
6.设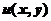 在平面有界闭区域D上连续,在D的内部具有二阶连续偏导数,且满足
在平面有界闭区域D上连续,在D的内部具有二阶连续偏导数,且满足 及
及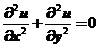 ,则( ).
,则( ).
(A)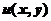 的最大值点和最小值点必定都在区域D的边界上;
的最大值点和最小值点必定都在区域D的边界上;
(B)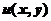 的最大值点和最小值点必定都在区域D的内部;
的最大值点和最小值点必定都在区域D的内部;
(C)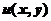 的最大值点在区域D的内部,最小值点在区域D的边界上;
的最大值点在区域D的内部,最小值点在区域D的边界上;
(D)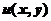 的最小值点在区域D的内部,最大值点在区域D的边界上.
的最小值点在区域D的内部,最大值点在区域D的边界上.
7.行列式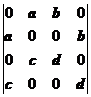 等于
等于
(A)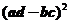 (B)
(B)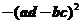 (C)
(C)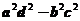 (D)
(D)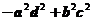
8.设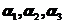 是三维向量,则对任意的常数
是三维向量,则对任意的常数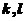 ,向量
,向量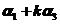 ,
,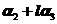 线性无关是向量
线性无关是向量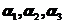 线性无关的
线性无关的
(A)必要而非充分条件 (B)充分而非必要条件
(C)充分必要条件 (D) 非充分非必要条件
二、填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上)
9.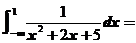 .
.
10.设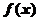 为周期为4的可导奇函数,且
为周期为4的可导奇函数,且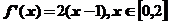 ,则
,则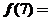 .
.
11.设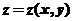 是由方程
是由方程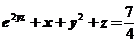 确定的函数,则
确定的函数,则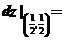 .
.
12.曲线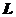 的极坐标方程为
的极坐标方程为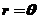 ,则
,则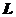 在点
在点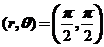 处的切线方程为 .
处的切线方程为 .
13.一根长为1的细棒位于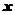 轴的区间
轴的区间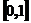 上,若其线密度
上,若其线密度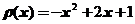 ,则该细棒的质心坐标
,则该细棒的质心坐标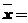 .
.
14.设二次型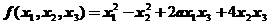 的负惯性指数是1,则
的负惯性指数是1,则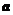 的取值范围是 .
的取值范围是 .
三、解答题
15.(本题满分10分)
求极限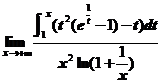 .
.
16.(本题满分10分)
已知函数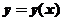 满足微分方程
满足微分方程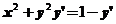 ,且
,且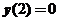 ,求
,求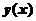 的极大值和极小值.
的极大值和极小值.
17.(本题满分10分)
设平面区域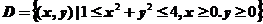 .计算
.计算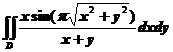
18.(本题满分10分)
设函数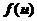 具有二阶连续导数,
具有二阶连续导数,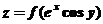 满足
满足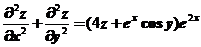 .若
.若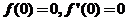 ,求
,求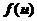 的表达式.
的表达式.
19.(本题满分10分)
设函数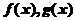 在区间
在区间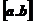 上连续,且
上连续,且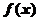 单调增加,
单调增加,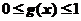 ,证明:
,证明:
(1)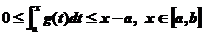 ;
;
(2)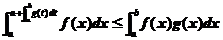 .
.
20.(本题满分11分)
设函数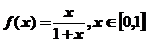 ,定义函数列
,定义函数列
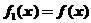 ,
,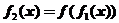 ,
,
设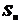 是曲线
是曲线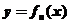 ,直线
,直线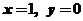 所围图形的面积.求极限
所围图形的面积.求极限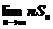 .
.
21.(本题满分11分)
已知函数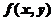 满足
满足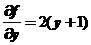 ,且
,且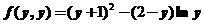 ,求曲线
,求曲线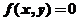 所成的图形绕直线
所成的图形绕直线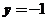 旋转所成的旋转体的体积.
旋转所成的旋转体的体积.
22.(本题满分11分)
设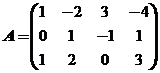 ,E为三阶单位矩阵.
,E为三阶单位矩阵.
(1)求方程组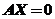 的一个基础解系;
的一个基础解系;
(2)求满足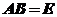 的所有矩阵.
的所有矩阵.
,
23.(本题满分11分)
证明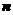 阶矩阵
阶矩阵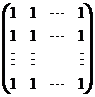 与
与 相似.
相似.
2014年考研数学二真题与解析
一、选择题 1—8小题.每小题4分,共32分.
1.当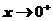 时,若
时,若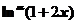 ,
,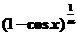 均是比
均是比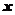 高阶的无穷小,则
高阶的无穷小,则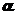 的可能取值范围是( )
的可能取值范围是( )
(A)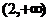 (B)
(B)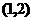 (C)
(C)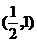 (D)
(D)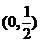
【详解】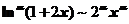 ,是
,是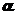 阶无穷小,
阶无穷小,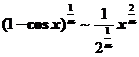 是
是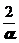 阶无穷小,由题意可知
阶无穷小,由题意可知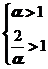
所以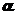 的可能取值范围是
的可能取值范围是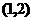 ,应该选(B).
,应该选(B).
2.下列曲线有渐近线的是
(A)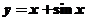 (B)
(B)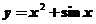 (C)
(C)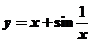 (D)
(D)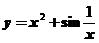
【详解】对于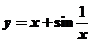 ,可知
,可知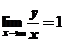 且
且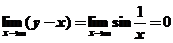 ,所以有斜渐近线
,所以有斜渐近线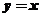
应该选(C)
3.设函数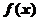 具有二阶导数,
具有二阶导数,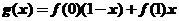 ,则在
,则在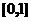 上( )
上( )
(A)当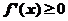 时,
时,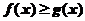 (B)当
(B)当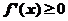 时,
时,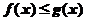
(C)当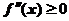 时,
时,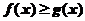 (D)当
(D)当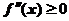 时,
时,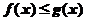
【分析】此题考查的曲线的凹凸性的定义及判断方法.
【详解1】如果对曲线在区间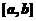 上凹凸的定义比较熟悉的话,可以直接做出判断. 显然
上凹凸的定义比较熟悉的话,可以直接做出判断. 显然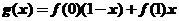 就是联接
就是联接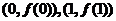 两点的直线方程.故当
两点的直线方程.故当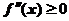 时,曲线是凹的,也就是
时,曲线是凹的,也就是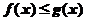 ,应该选(D)
,应该选(D)
【详解2】如果对曲线在区间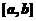 上凹凸的定义不熟悉的话,可令
上凹凸的定义不熟悉的话,可令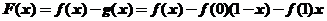 ,则
,则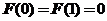 ,且
,且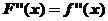 ,故当
,故当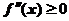 时,曲线是凹的,从而
时,曲线是凹的,从而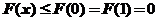 ,即
,即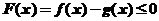 ,也就是
,也就是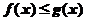 ,应该选(D)
,应该选(D)
4.曲线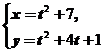 上对应于
上对应于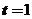 的点处的曲率半径是( )
的点处的曲率半径是( )
(A)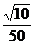 (B)
(B)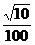 (C)
(C)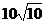 (D)
(D)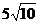
【详解】 曲线在点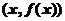 处的曲率公式
处的曲率公式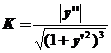 ,曲率半径
,曲率半径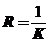 .
.
本题中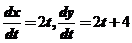 ,所以
,所以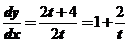 ,
,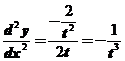 ,
,
对应于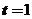 的点处
的点处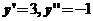 ,所以
,所以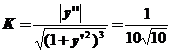 ,曲率半径
,曲率半径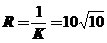 .
.
应该选(C)
5.设函数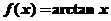 ,若
,若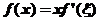 ,则
,则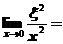 ( )
( )
(A)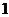 (B)
(B)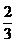 (C)
(C)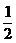 (D)
(D)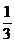
【详解】注意(1)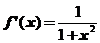 ,(2)
,(2)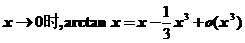 .
.
由于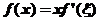 .所以可知
.所以可知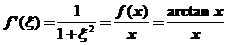 ,
,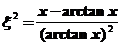 ,
,
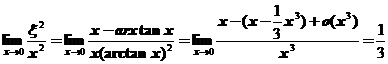 .
.
6.设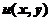 在平面有界闭区域D上连续,在D的内部具有二阶连续偏导数,且满足
在平面有界闭区域D上连续,在D的内部具有二阶连续偏导数,且满足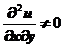 及
及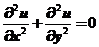 ,则( ).
,则( ).
(A)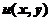 的最大值点和最小值点必定都在区域D的边界上;
的最大值点和最小值点必定都在区域D的边界上;
(B)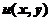 的最大值点和最小值点必定都在区域D的内部;
的最大值点和最小值点必定都在区域D的内部;
(C)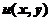 的最大值点在区域D的内部,最小值点在区域D的边界上;
的最大值点在区域D的内部,最小值点在区域D的边界上;
(D)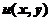 的最小值点在区域D的内部,最大值点在区域D的边界上.
的最小值点在区域D的内部,最大值点在区域D的边界上.
【详解】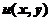 在平面有界闭区域D上连续,所以
在平面有界闭区域D上连续,所以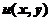 在D内必然有最大值和最小值.并且如果在内部存在驻点
在D内必然有最大值和最小值.并且如果在内部存在驻点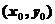 ,也就是
,也就是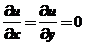 ,在这个点处
,在这个点处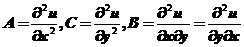 ,由条件,显然
,由条件,显然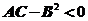 ,显然
,显然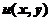 不是极值点,当然也不是最值点,所以
不是极值点,当然也不是最值点,所以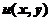 的最大值点和最小值点必定都在区域D的边界上.
的最大值点和最小值点必定都在区域D的边界上.
所以应该选(A).
7.行列式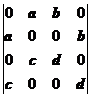 等于
等于
(A)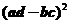 (B)
(B)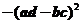 (C)
(C)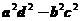 (D)
(D)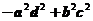
【详解】
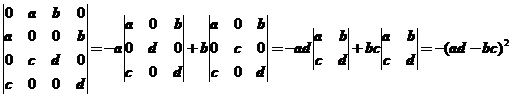
应该选(B).
8.设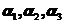 是三维向量,则对任意的常数
是三维向量,则对任意的常数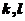 ,向量
,向量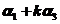 ,
,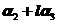 线性无关是向量
线性无关是向量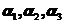 线性无关的
线性无关的
(A)必要而非充分条件 (B)充分而非必要条件
(C)充分必要条件 (D) 非充分非必要条件
【详解】若向量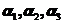 线性无关,则
线性无关,则
(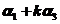 ,
,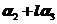 )
)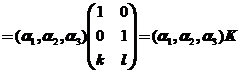 ,对任意的常数
,对任意的常数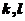 ,矩阵
,矩阵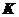 的秩都等于2,所以向量
的秩都等于2,所以向量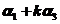 ,
,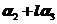 一定线性无关.
一定线性无关.
而当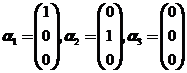 时,对任意的常数
时,对任意的常数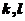 ,向量
,向量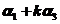 ,
,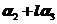 线性无关,但
线性无关,但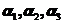 线性相关;故选择(A).
线性相关;故选择(A).
二、填空题(本题共6小题,每小题4分,满分24分. 把答案填在题中横线上)
9.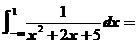 .
.
【详解】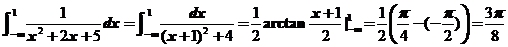 .
.
10.设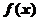 为周期为4的可导奇函数,且
为周期为4的可导奇函数,且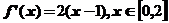 ,则
,则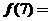 .
.
【详解】当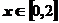 时,
时,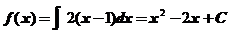 ,由
,由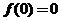 可知
可知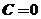 ,即
,即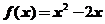 ;
;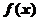 为周期为4奇函数,故
为周期为4奇函数,故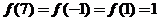 .
.
11.设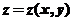 是由方程
是由方程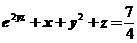 确定的函数,则
确定的函数,则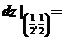 .
.
【详解】设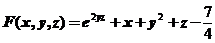 ,
,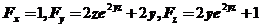 ,当
,当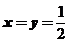 时,
时,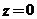 ,
,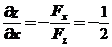 ,
,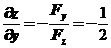 ,所以
,所以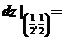
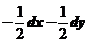 .
.
12.曲线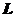 的极坐标方程为
的极坐标方程为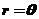 ,则
,则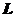 在点
在点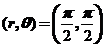 处的切线方程为 .
处的切线方程为 .
【详解】先把曲线方程化为参数方程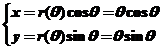 ,于是在
,于是在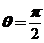 处,
处,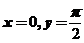 ,
,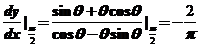 ,则
,则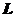 在点
在点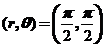 处的切线方程为
处的切线方程为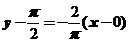 ,即
,即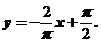
13.一根长为1的细棒位于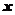 轴的区间
轴的区间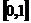 上,若其线密度
上,若其线密度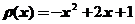 ,则该细棒的质心坐标
,则该细棒的质心坐标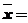 .
.
【详解】质心坐标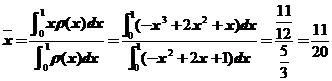 .
.
14.设二次型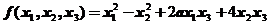 的负惯性指数是1,则
的负惯性指数是1,则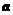 的取值范围是 .
的取值范围是 .
【详解】由配方法可知
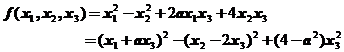
由于负惯性指数为1,故必须要求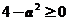 ,所以
,所以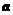 的取值范围是
的取值范围是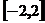 .
.
三、解答题
15.(本题满分10分)
求极限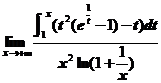 .
.
【分析】.先用等价无穷小代换简化分母,然后利用洛必达法则求未定型极限.
【详解】
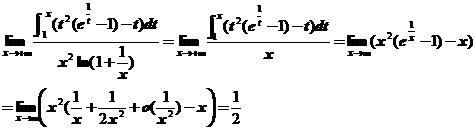
16.(本题满分10分)
已知函数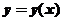 满足微分方程
满足微分方程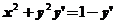 ,且
,且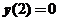 ,求
,求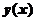 的极大值和极小值.
的极大值和极小值.
【详解】
解:把方程化为标准形式得到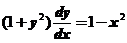 ,这是一个可分离变量的一阶微分方程,两边分别积分可得方程通解为:
,这是一个可分离变量的一阶微分方程,两边分别积分可得方程通解为: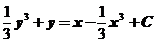 ,由
,由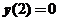 得
得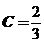 ,
,
即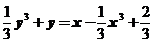 .
.
令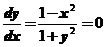 ,得
,得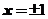 ,且可知
,且可知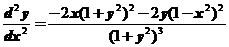 ;
;
当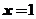 时,可解得
时,可解得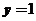 ,
,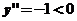 ,函数取得极大值
,函数取得极大值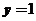 ;
;
当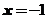 时,可解得
时,可解得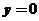 ,
,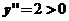 ,函数取得极小值
,函数取得极小值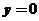 .
.
17.(本题满分10分)
设平面区域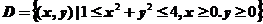 .计算
.计算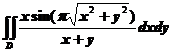
【详解】由对称性可得
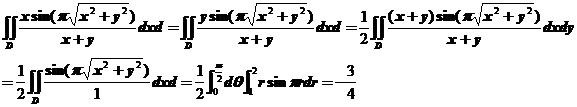
18.(本题满分10分)
设函数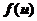 具有二阶连续导数,
具有二阶连续导数,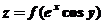 满足
满足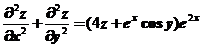 .若
.若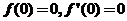 ,求
,求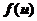 的表达式.
的表达式.
【详解】
设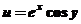 ,则
,则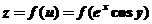 ,
,
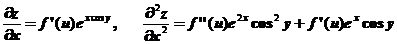 ;
;
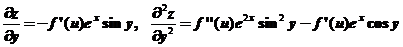 ;
;
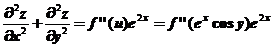
由条件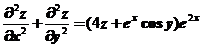 ,
,
可知
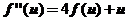
这是一个二阶常用系数线性非齐次方程.
对应齐次方程的通解为:
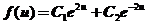 其中
其中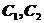 为任意常数.
为任意常数.
对应非齐次方程特解可求得为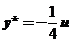 .
.
故非齐次方程通解为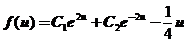 .
.
将初始条件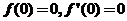 代入,可得
代入,可得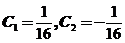 .
.
所以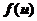 的表达式为
的表达式为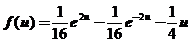 .
.
19.(本题满分10分)
设函数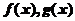 在区间
在区间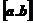 上连续,且
上连续,且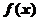 单调增加,
单调增加,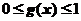 ,证明:
,证明:
(1) 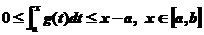 ;
;
(2) 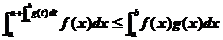 .
.
【详解】
(1)证明:因为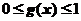 ,所以
,所以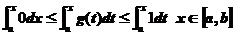 .
.
即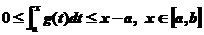 .
.
(2)令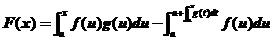 ,
,
则可知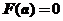 ,且
,且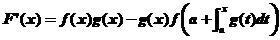 ,
,
因为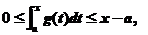 且
且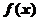 单调增加,
单调增加,
所以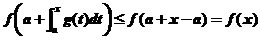 .从而
.从而
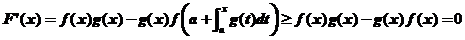 ,
, 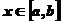
也是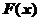 在
在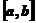 单调增加,则
单调增加,则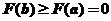 ,即得到
,即得到
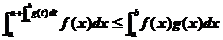 .
.
20.(本题满分11分)
设函数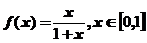 ,定义函数列
,定义函数列
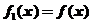 ,
,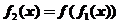 ,
,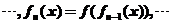
设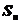 是曲线
是曲线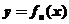 ,直线
,直线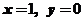 所围图形的面积.求极限
所围图形的面积.求极限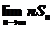 .
.
【详解】
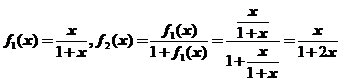 ,
,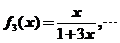 ,
,
利用数学归纳法可得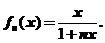
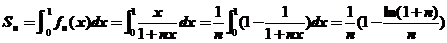 ,
,
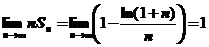 .
.
21.(本题满分11分)
已知函数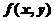 满足
满足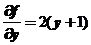 ,且
,且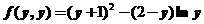 ,求曲线
,求曲线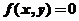 所成的图形绕直线
所成的图形绕直线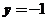 旋转所成的旋转体的体积.
旋转所成的旋转体的体积.
【详解】
由于函数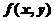 满足
满足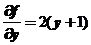 ,所以
,所以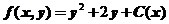 ,其中
,其中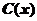 为待定的连续函数.
为待定的连续函数.
又因为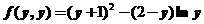 ,从而可知
,从而可知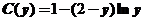 ,
,
得到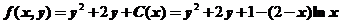 .
.
令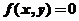 ,可得
,可得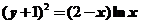 .且当
.且当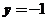 时,
时,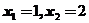 .
.
曲线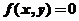 所成的图形绕直线
所成的图形绕直线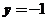 旋转所成的旋转
旋转所成的旋转