微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
的秩为1,则必有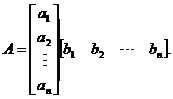
(6).. 【分析】 先化简分解出矩阵B,再取行列式即可.
【详解】 由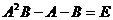 知,
知,
 ,即
,即 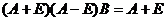 ,
,
易知矩阵A+E可逆,于是有 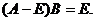
再两边取行列式,得 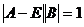 ,
,
因为 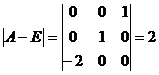 , 所以
, 所以 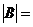
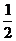 .
.
二、选择题(本题共6小题,每小题4分,满分24分. 每小题给出的四个选项中,只有一项符合题目要求,把所选项前的字母填在题后的括号内)
(1). 【分析】 本题考查极限概念,极限值与数列前面有限项的大小无关,可立即排除(A),(B); 而极限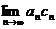 是
是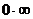 型未定式,可能存在也可能不存在,举反例说明即可;极限
型未定式,可能存在也可能不存在,举反例说明即可;极限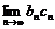 属
属 型,必为无穷大量,即不存在.
型,必为无穷大量,即不存在.
【详解】 用举反例法,取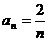 ,
,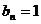 ,
,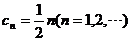 ,则可立即排除(A),(B),(C),因此正确选项为(D).
,则可立即排除(A),(B),(C),因此正确选项为(D).
【评注】 对于不便直接证明的问题,经常可考虑用反例,通过排除法找到正确选项. 完全类似方法见《数学最后冲刺》P.179.
(2). 【分析】 先用换元法计算积分,再求极限.
【详解】 因为
 =
=
= ,
,
可见  =
=
【评注】 本题属常规题型,综合考查了定积分计算与求数列的极限两个知识点,但定积分和数列极限的计算均是最基础的问题,一般教材中均可找到其计算方法.
(3). 【分析】 将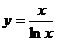 代入微分方程,再令
代入微分方程,再令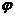 的中间变量为u,求出
的中间变量为u,求出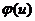 的表达式,进而可计算出
的表达式,进而可计算出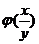 .
.
【详解】将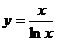 代入微分方程
代入微分方程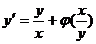 ,得
,得
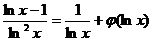 ,即
,即 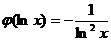 .
.
令 lnx=u,有 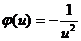 ,故
,故 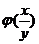 =
= 应选(A).
应选(A).
【评注】 本题巧妙地将微分方程的解与求函数关系结合起来,具有一定的综合性,但问题本身并不复杂,只要仔细计算应该可以找到正确选项.
(4). 【分析】 答案与极值点个数有关,而可能的极值点应是导数为零或导数不存在的点,共4个,是极大值点还是极小值可进一步由取极值的第一或第二充分条件判定.
【详解】 根据导函数的图形可知,一阶导数为零的点有3个,而 x=0 则是导数不存在的点. 三个一阶导数为零的点左右两侧导数符号不一致,必为极值点,且两个极小值点,一个极大值点;在x=0左侧一阶导数为正,右侧一阶导数为负,可见x=0为极大值点,故f(x)共有两个极小值点和两个极大值点,应选(C).
【评注】 本题属新题型,类似考题2001年数学一、二中曾出现过,当时考查的是已知f(x)的图象去推导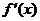 的图象,本题是其逆问题. 完全类似例题在文登学校经济类串讲班上介绍过
的图象,本题是其逆问题. 完全类似例题在文登学校经济类串讲班上介绍过
.(5). 【分析】 直接计算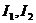 是困难的,可应用不等式tanx>x, x>0.
是困难的,可应用不等式tanx>x, x>0.
【详解】 因为当 x>0 时,有tanx>x,于是 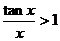 ,
,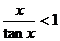 ,从而有
,从而有 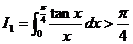 ,
, 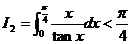 ,
,
可见有 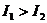 且
且 ,可排除(A),(C),(D),故应选(B).
,可排除(A),(C),(D),故应选(B).
【评注】 本题没有必要去证明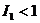 ,因为用排除法,(A),(C),(D)均不正确,剩下的(B) 一定为正确选项.
,因为用排除法,(A),(C),(D)均不正确,剩下的(B) 一定为正确选项.
(6) 【分析】 本题为一般教材上均有的比较两组向量个数的定理:若向量组I: 可由向量组II:
可由向量组II: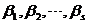 线性表示,则当
线性表示,则当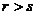 时,向量组I必线性相关. 或其逆否命题:若向量组I:
时,向量组I必线性相关. 或其逆否命题:若向量组I: 可由向量组II:
可由向量组II: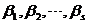 线性表示,且向量组I线性无关,则必有
线性表示,且向量组I线性无关,则必有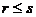 . 可见正确选项为(D). 本题也可通过举反例用排除法找到答案.
. 可见正确选项为(D). 本题也可通过举反例用排除法找到答案.
【详解】 用排除法:如 ,则
,则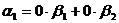 ,但
,但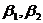 线性无关,排除(A);
线性无关,排除(A); ,则
,则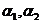 可由
可由 线性表示,但
线性表示,但 线性无关,排除(B);
线性无关,排除(B);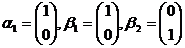 ,
,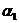 可由
可由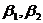 线性表示,但
线性表示,但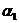 线性无关,排除(C). 故正确选项为(D).
线性无关,排除(C). 故正确选项为(D).
【评注】 本题将一已知定理改造成选择题,如果考生熟知此定理应该可直接找到答案,若记不清楚,也可通过构造适当的反例找到正确选项。
三 、(本题满分10分)
【分析】 分段函数在分段点x=0连续,要求既是左连续又是右连续,即

【详解】 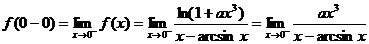
=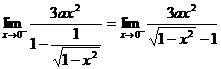
=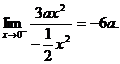

=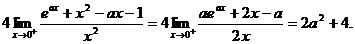
令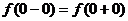 ,有
,有 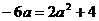 ,得
,得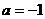 或
或 .
.
当a=-1时,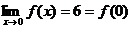 ,即f(x)在x=0处连续.
,即f(x)在x=0处连续.
当a=-2时,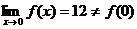 ,因而x=0是f(x)的可去间断点.
,因而x=0是f(x)的可去间断点.
【评注】 本题为基本题型,考查了极限、连续与间断等多个知识点,其中左右极限的计算有一定难度,在计算过程中应尽量利用无穷小量的等价代换进行简化.
四. 【分析】 本题为参数方程求二阶导数,按参数方程求导的公式进行计算即可. 注意当x=9 时,可相应地确定参数t的取值.
【详解】由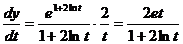 ,
,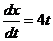 ,
,
得 
所以 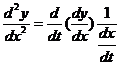 =
=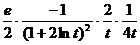
=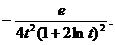
当x=9时,由 及t>1得t=2, 故
及t>1得t=2, 故
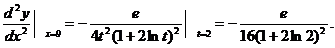
五. 【分析】 被积函数含有根号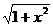 ,典型地应作代换:x=tant, 或被积函数含有反三角函数arctanx,同样可考虑作变换:arctanx=t,即 x=tant.
,典型地应作代换:x=tant, 或被积函数含有反三角函数arctanx,同样可考虑作变换:arctanx=t,即 x=tant.
【详解】 设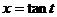 ,则
,则
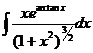 =
=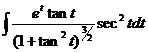 =
=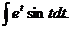
又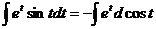
=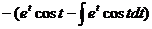
=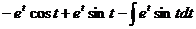 ,
,
故 
因此 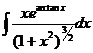 =
=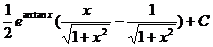
=
【评注】本题也可用分布积分法:
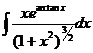 =
=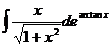
=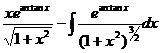
=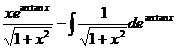
=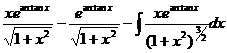 ,
,
移项整理得
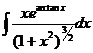 =
=
本题的关键是含有反三角函数,作代换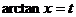 或tant=x, 完全类似例题见《数学复习指南》P.86【例3.23】以及P.90习题12.
或tant=x, 完全类似例题见《数学复习指南》P.86【例3.23】以及P.90习题12.
六. 【分析】 将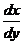 转化为
转化为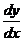 比较简单,
比较简单,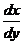 =
=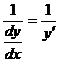 ,关键是应注意:
,关键是应注意:
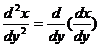 =
=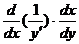
= .
.
然后再代入原方程化简即可.
【详解】 (1) 由反函数的求导公式知 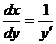 ,于是有
,于是有
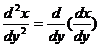 =
=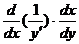 =
= .
.
代入原微分方程得
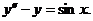 ( * )
( * )
(2) 方程( * )所对应的齐次方程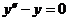 的通解为
的通解为
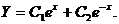
设方程( * )的特解为
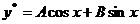 ,
,
代入方程( * ),求得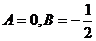 ,故
,故 ,从而
,从而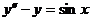 的通解是
的通解是
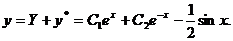
由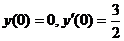 ,得
,得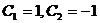 . 故所求初值问题的解为
. 故所求初值问题的解为
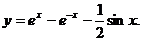
【评注】 本题的核心是第一步方程变换,完全类似例题见《数学复习指南》P.53的【例2.8】和P.59的【例2.22】.
七. 【分析】 问题等价于讨论方程 有几个不同的实根. 本题相当于一函数作图题,通过单调性、极值的讨论即可确定实根的个数(与x轴交点的个数).
有几个不同的实根. 本题相当于一函数作图题,通过单调性、极值的讨论即可确定实根的个数(与x轴交点的个数).
 【详解】 设
【详解】 设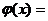
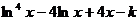 , y
, y




 则有
则有 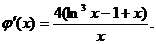 4-k
4-k
 不难看出,x=1是
不难看出,x=1是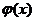 的驻点. O 1 x
的驻点. O 1 x
当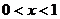 时,
时,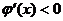 ,即
,即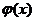 单调减少;当x>1时,
单调减少;当x>1时,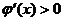 ,即
,即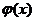 单调增加,故
单调增加,故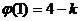 为函数
为函数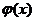 的最小值.
的最小值.
当k<4,即4-k>0时,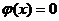 无实根,即两条曲线无交点;
无实根,即两条曲线无交点;
当 k=4,即4-k=0时,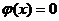 有唯一实根,即两条曲线只有一个交点;
有唯一实根,即两条曲线只有一个交点;
当 k>4,即4-k<0时,由于
 ;
;
 ,
,
故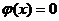 有两个实根,分别位于(0,1)与
有两个实根,分别位于(0,1)与 内,即两条曲线有两个交点.
内,即两条曲线有两个交点.
【评注】 讨论曲线与坐标轴的交点,在构造辅助函数时,应尽量将待分析的参数分离开来,使得求导后不含参数,便于求驻点坐标.
八.. 【分析】 (1) 先求出法线方程与交点坐标Q,再由题设线段PQ被x轴平分,可转化为微分方程,求解此微分方程即可得曲线y=f(x)的方程. (2) 将曲线 y=f(x) 化为参数方程,再利用弧长公式 进行计算即可.
进行计算即可.
【详解】 (1) 曲线y=f(x)在点P(x,y)处的法线方程为
 ,
,
其中(X,Y)为法线上任意一点的坐标. 令X=0,则
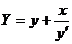 ,
,
故Q点的坐标为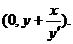 由题设知
由题设知
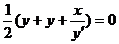 ,即
,即 
积分得 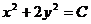 (C为任意常数).
(C为任意常数).
由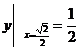 知C=1,故曲线y=f(x)的方程为
知C=1,故曲线y=f(x)的方程为
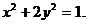
(2) 曲线y=sinx在[0,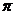 ]上的弧长为
]上的弧长为

曲线y=f(x)的参数方程为