|
微信搜索关注"91考试网"公众号,领30元,获取公务员、事业编、教师等考试资料40G!
p; 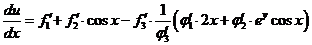 . .
【相关知识点】多元复合函数求导法则:如果函数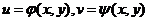 都在点 都在点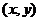 具有对 具有对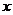 及对 及对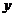 的偏导数,函数 的偏导数,函数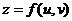 在对应点 在对应点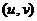 具有连续偏导数,则复合函数 具有连续偏导数,则复合函数
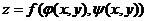 在点 在点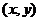 的两个偏导数存在,且有 的两个偏导数存在,且有
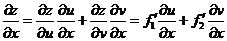 ; ;
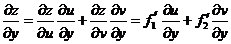 . .
 (2)【解析】方法一:用重积分的方法. (2)【解析】方法一:用重积分的方法.
将累次积分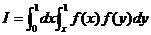 表成二重积分 表成二重积分
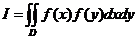 , ,
其中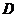 如右图所示.交换积分次序 如右图所示.交换积分次序
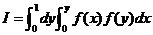 . .
由于定积分与积分变量无关,改写成
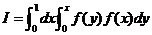 . .
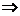 

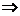 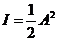 . .
方法二:用分部积分法.
注意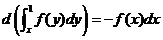 ,将累次积分 ,将累次积分 写成 写成

四、(本题共2小题,每小题6分,满分12分.)
(1)【解析】将曲面积分 化为二重积分 化为二重积分 . .
首先确定被积函数 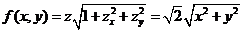 , ,
对锥面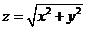 而言, 而言, 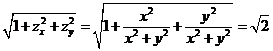 . .
 其次确定积分区域即 其次确定积分区域即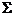 在 在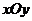 平面的投影区域 平面的投影区域
(见右图),按题意:
 ,即 ,即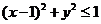 . .
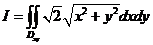 . .
作极坐标变换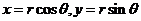 ,则 ,则
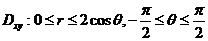 , ,
因此  . .
(2)【解析】这就是将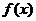 作偶延拓后再作周期为4的周期延拓.于是得 作偶延拓后再作周期为4的周期延拓.于是得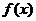 的傅氏系数: 的傅氏系数:


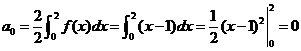 . .
由于(延拓后)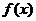 在 在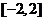 分段单调、连续且 分段单调、连续且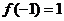 .于是 .于是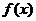 有展开式 有展开式
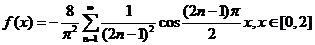 . .
五、(本题满分7分)
【解析】设点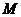 的坐标为 的坐标为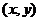 ,则 ,则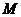 处的切线方程为 处的切线方程为 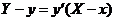 . .
令 ,得 ,得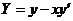 ,切线与 ,切线与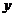 轴的交点为 轴的交点为 .由 .由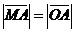 ,有 ,有
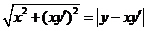 . .
化简后得伯努利方程 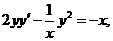 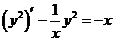 . .
令 ,方程化为一阶线性方程 ,方程化为一阶线性方程 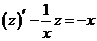 . .
解得  ,即 ,即 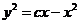 ,亦即 ,亦即  . .
又由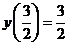 ,得 ,得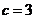 , ,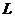 的方程为 的方程为 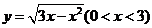 . .
六、(本题满分8分)
【解析】在平面上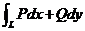 与路径无关(其中 与路径无关(其中 有连续偏导数), 有连续偏导数),
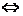 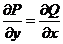 ,即 ,即 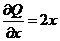 . .
对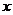 积分得 积分得 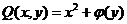 ,其中 ,其中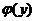 待定.代入另一等式得对 待定.代入另一等式得对 , ,
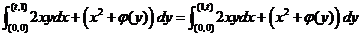 . ① . ①
下面由此等式求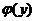 . .
方法一:易求得原函数

于是由①式得 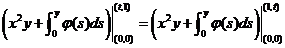 . .
即  ,亦即 ,亦即  . .
求导得  ,即 ,即 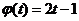 . .
因此  . .
方法二:取特殊的积分路径:对①式左端与右端积分分别取积分路径如下图所示.
于是得 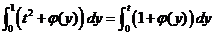 . .
即  ,亦即 ,亦即 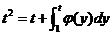 . .
其余与方法一相同.
七、(本题满分8分)
【解析】(1)反证法.假设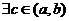 ,使 ,使 .则由罗尔定理, .则由罗尔定理,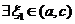 与 与
使 ;从而由罗尔定理, ;从而由罗尔定理,  , ,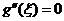 .这与 .这与
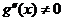 矛盾. 矛盾.
(2)证明本题的关键问题是:“对谁使用罗尔定理?”换言之,“谁的导数等于零?”
这应该从所要证明的结果来考察.由证明的结果可以看出本题即证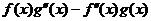 在 在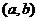 存在零点. 存在零点.
方法一:注意到 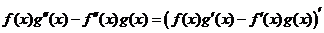 , ,
考察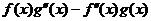 的原函数,令 的原函数,令
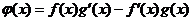 , ,
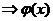 在 在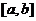 可导, 可导, .由罗尔定理, .由罗尔定理,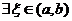 ,使 ,使 .即有 .即有
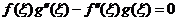 ,亦即 ,亦即 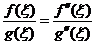 . .
方法二:若不能像前面那样观察到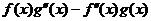 的原函数,我们也可以用积分来讨论这个问题: 的原函数,我们也可以用积分来讨论这个问题:
 . .


 (取 (取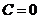 ). ).
令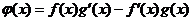 ,其余与方法一相同. ,其余与方法一相同.
八、(本题满分7分)
【解析】设对应于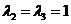 的特征向量为 的特征向量为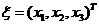 ,因为 ,因为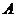 为实对称矩阵,且实对称矩阵的不同特征值所对应的特征向量相互正交,故 为实对称矩阵,且实对称矩阵的不同特征值所对应的特征向量相互正交,故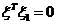 ,即 ,即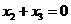 . .
解之得 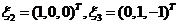 . .
于是有 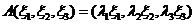 , ,
所以 
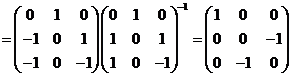 . .
九、(本题满分6分)
【解析】方法一:根据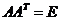 有 有
 , ,
移项得 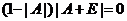 . .
因为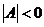 ,故 ,故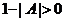 .所以 .所以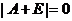 . .
方法二:因为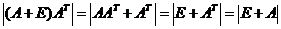 , ,
所以 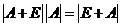 , ,
即 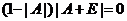 . .
因为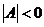 ,故 ,故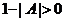 .所以 .所以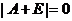 . .
十、填空题(本题共2小题,每小题3分,满分6分.)
(1)【解析】由题设,因为是独立重复实验,所以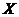 服从 服从 的二项分布. 的二项分布.
由二项分布的数学期望和方差计算公式,有
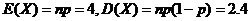 , ,
根据方差性质有 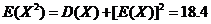 . .
(2)【解析】令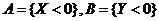 ,则 ,则
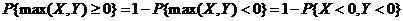 . .
由概率的广义加法公式  ,有 ,有


十一、(本题满分6分)
【解析】方法1:用分布函数法先求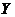 的分布函数 的分布函数 . .
当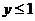 时, 时, 
当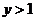 时, 时,  

所以由连续型随机变量的概率密度是分布函数的微分,得

或者直接将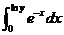 对 对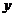 求导数得 求导数得
方法2:用单调函数公式直接求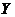 的概率密度. 的概率密度.
由于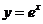 在 在 内单调,其反函数 内单调,其反函数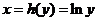 在 在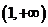 内可导且其导数为 内可导且其导数为
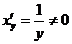 ,则所求概率密度函数为 ,则所求概率密度函数为
 
【相关知识点】对积分上限的函数的求导公式:
若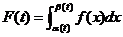 , ,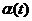 , ,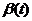 均一阶可导,则 均一阶可导,则
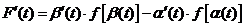 . .
|