1、某次抽奖活动在三个箱子中均放有红、黄、一绿、蓝、紫、橙、白、黑8种颜色的球各一个,奖励规则如下:从三个箱子中分别摸出一个球,摸出的3个球均为红球的得一等奖,摸出的3个球中至少有一个绿球的得二等奖,摸出的3个球均为彩色球(黑、白除外)的得三等奖。问不中奖的概率是多少?_____
A: 在 0~25%之间B: 在25~50%之间C: 在50~75%之间D: 在75~100%之间
参考答案: C 本题解释:C。
2、地球表面的陆地面积和海洋面积之比是29:71,其中陆地的四分之三在北半球,那么南、北半球海洋面积之比是_____。
A: 284:29B: 113:55C: 371:313D: 171:113
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析根据题干中的比例关系,可以推断出南、北半球的海洋面积之比为:(50-29×0.25):(50-29×0.75)=42.75:28.25=171:113。故正确答案为D。
3、一个小于200的数,它除以11余8,除以13余10,那么这个数是多少?_____
A: 118B: 140C: 153D: 162
参考答案: B 本题解释:参考答案:B题目详解:方法一:根据差同公式:被除数=几个除数的最小公倍数的倍数-除数与余数的差: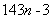 ,又小于200的数,选B;方法二:设这个数为P,P除以11余8,则
,又小于200的数,选B;方法二:设这个数为P,P除以11余8,则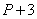 是11的倍数:P除以13余10,则
是11的倍数:P除以13余10,则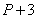 是13的倍数。综上,
是13的倍数。综上,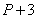 就是1l、13的公倍数,11、13的最小公倍数为143,那么小于200的数中,P就是140;考查点:数量关系>数学运算>计算问题之数的性质>余数问题>一个被除数,多个除数>特殊形式>差同
就是1l、13的公倍数,11、13的最小公倍数为143,那么小于200的数中,P就是140;考查点:数量关系>数学运算>计算问题之数的性质>余数问题>一个被除数,多个除数>特殊形式>差同
4、某商场开展购物优惠活动:一次购买300元及以下的商品九折优惠;一次购买300元以上的商品,其中300元九折优惠,超过的部分八折优惠。小王购物第一次付款144元,第二次又付款310元。如果他一次购买并付款,可以节省多少元?_____
A: 16B: 22.4C: 30.6D: 48
参考答案: A 本题解释:正确答案是A考点统筹规划问题解析第一次付款144元,可得这部分商品原价为160元;第二次付款超过300元,可知这部分商品原价肯定超过300元,所以这部分不论合并还是不合并,都是付款310元。只有第一次付款的部分由九折变为八折,所以节省160×(0.9-0.8)=16元。故正确答案为A。
5、小王收购了一台旧电视机,然后转手卖出,赚取了30%的利润。1个月后,客户要求退货,小王和客户达成协议,以当时交易价格的90%回收了这台电视机,后来小王又以最初的收购价格其卖出。问小王在这台电视机交易中的利润率为_____。
A: 13%B: 17%C: 20%D: 27%
参考答案: A 本题解释:正确答案是A考点经济利润问题解析直接赋值,设收购价为100,则利润为30,出售价为130;后以90%出售价回收即117,又以收购价100卖出,亏损17;故小王在这台电视机交易中的利润率为(30-17)÷100=13%。故正确答案为A。标签赋值思想
6、甲从A地步行到B地,出发1小时40分钟后,乙骑自行车也从同地出发,骑了10公里时追到甲。于是,甲改骑乙的自行车前进,共经5小时到达B地,这恰是甲步行全程所需时间的一半。问骑自行车的速度是多少公里/小时?_____
A: 12B: 10C: 16D: 15
参考答案: A 本题解释:正确答案是A考点行程问题解析根据已知,10公里的路程骑车比步行省1小时40分(100分钟)。甲骑车后比全程步行省了5小时(前段路程是步行,没有节省),也就是300分钟,说明甲后来骑车了3×10=30公里。从A到B的路程总共是10+30=40公里。全程骑车共需要300-100=200分钟=10/3小时,所以骑车速度=40/(10/3)=12公里/小时,故正确答案为A。
7、小白兔说:“妈妈,我到您现在这么大时,您就13岁啦。”大白兔说:“我像你这么大年龄时,你只有1岁。”请问小白兔现在几岁?_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:参考答案:B题目详解:解法一:平均分段法:13与1相隔12,平均分成了3个4,可得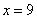 ,
, 。
。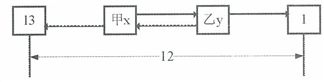 解法二:直接采用代入法:以A为例,如果小白兔4岁,那么大白兔四岁时候小白兔1岁,由此推出大白兔比小白兔大三岁,即大白兔7岁。小白兔要是像大白兔那么大的时候小白兔就是7岁,那么大白兔就应该是10岁。与题干13岁不符合,故A错。同种方法,B对。考查点:数量关系>数学运算>特殊情境问题>年龄问题
解法二:直接采用代入法:以A为例,如果小白兔4岁,那么大白兔四岁时候小白兔1岁,由此推出大白兔比小白兔大三岁,即大白兔7岁。小白兔要是像大白兔那么大的时候小白兔就是7岁,那么大白兔就应该是10岁。与题干13岁不符合,故A错。同种方法,B对。考查点:数量关系>数学运算>特殊情境问题>年龄问题
8、李森在一次村委会选举中,需2/3的选票才能当选,当统计完3/5的选票时,他得到的选票数已达到当选票数的3/4,它还需要得到剩下选票的几分之几才能当选?_____
A: 2500B: 3115C: 2225D: 2550
参考答案: C 本题解释:正确答案是D考点倍数约数问题解析75=3×5×5,共6个约数,质因数每多个3则约数多3个,质因数每多个5则约数多2个,所以A=3×3×3×5×5=675,B=3×5×5×5×5=1875,A+B=2550,故正确答案为D。秒杀技由题意可知,A和B均能被3整除,则其和也能被3整除,仅选项D符合,故正确答案为D。
9、某人做一道整数减法题时,把减数个位上的3看成了8,把减数十位上的8看成了3,得到的差是122,那么正确的得数应该是_____。
A: 77B: 88C: 90D: 100
参考答案: A 本题解释:参考答案:A题目详解:先求原来的减数:假设原来的减数是83,被误当做38,再求被减数:被减数应为122+38=160,则正确的得数为160-83=77。所以,选A.考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的排列与位数关系
10、计算从1到100(包括100)能被5整除得所有数的和?_____
A: 1100B: 1150C: 1200D: 1050
参考答案: D 本题解释:参考答案 题目详解:解法一:能被5整除的数构成一个等差数列即5、10、15…100。
题目详解:解法一:能被5整除的数构成一个等差数列即5、10、15…100。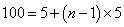

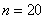 说明有这种性质的数总共为20个,所以和为
说明有这种性质的数总共为20个,所以和为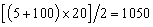 。解法二:能被5整除的数的尾数或是0、或是5,找出后相加。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除的性质
。解法二:能被5整除的数的尾数或是0、或是5,找出后相加。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除的性质
11、100张多米诺骨牌整齐地排成一列,依顺序编号为1、2、3……99,100.第一次拿走所有奇数位置上的骨牌,第二次再从剩余骨牌中拿走所有奇数位置上的骨牌,依此类推。请问最后剩下的一张骨牌的编号是多少?_____
A: 32B: 64C: 88D: 96
参考答案: B 本题解释:B。【解析】本题关键是理解题意,第一次拿走的是所有奇数,第二次拿走的各项是2分别乘以1、3、5、7、9……,依次类推,每拿走一次后,剩下的第一个数是20、21,22、23、24……,在100之内要使2n取值最大,所以最后剩下的是64,选B。
12、小王从家开车上班,其实行驶10分钟后发生了故障,小王从后备箱中取出自行车继续赶路,由于自行车的车速只有汽车的3/5,小王比预计时间晚了20分钟到达单位,如果之前汽车再多行驶6公里,他就能少迟到10分钟,从小王家到单位的距离是_____公里。
A: 12B: 14C: 15D: 16
参考答案: D 本题解释:正确答案是D考点行程问题解析由题意可知,汽车和自行车的速度之比为5:3,因此相同路程下汽车和自行车的用时之比为3:5。迟到20分钟,则余下的路程汽车30分钟,自行车50分钟,所以总路程开车需40分钟;迟到10分钟,则余下的路程汽车15分钟,自行车25分钟,后面一种情况比前面一种汽车多开了15分钟,行驶了6公里,因此全程的距离为6÷15×40=16公里,故正确答案为D。标签比例转化
13、0, 1, 1, 1, 2, 2, 3, 4八个数字做成的八位数,共可做成______个。_____
A: 2940B: 3040C: 3142D: 3144
参考答案: A 本题解释:A【解析】不妨先把这8个数字看作互不相同的数字,0暂时也不考虑是否能够放在最高位,那么这组数字的排列就是P(8,8),但是,事实上里面有3个1,和2个2,3个1在P(8,8)中是把它作为不同的数字排列的,那就必须从P(8,8)中扣除3个1的全排列P(3,3),因为全排列是分步完成的,在排列组合中,分步相乘,分类相加。可见必须通过除掉P(3,3)才能去掉这部分重复的数字形成的重复排列。2个2当然也是如此,所以不考虑0作为首位的情况是 P88/(P33×P22)。现在再来单独考虑0作为最高位的情况有多少种:P77/(P33×P22),最后结果就是:P88/(P33×P22)-P77/(P33×P22)=2940。
14、某市为合理用电,鼓励各用户安装峰谷电表,市原电价每度0.53元,改新表后,每晚10点至次日早8点为低谷,每度收0.28元,其余时间为高峰期,每度0.56元,为改装新电表每个用户须收取100元改装费,假定某用户每月用200度电,两个不同时段用电量各为100度,那么改装电表12个月后,该用户可节约_____元。
A: 161B: 162C: 163D: 164
参考答案: D 本题解释:正确答案是D考点经济利润问题解析电表改装之前该用户每年的用电费用为200×0.53×12=1272元;改装电表之后,该用户这一年的用电费用加上改装费用共(0.28×100+0.56×100)×12+100=1108元,该用户改装电表前后可节约1272-1108=164元。故正确答案为D。
15、一群人坐车旅游,每辆车坐22人,剩5人没有座位,每辆坐26人,空出5个座位, 问每辆车坐25人,空出多少座位? _____
A: 20B: 15C: 10D: 5
参考答案: C 本题解释: C。一盈一亏型,车的数量为(15+5)÷ (26-22)=5,则共有5×22+5=115人。则坐25人时,115 ÷ 25=4……15,即需要5辆车,空出25-15=10个座位。
16、在一次国际美食大赛中,中、法、日、俄四国的评委对一道菜品进行打分。中国评委和法国评委给出的平均分是94,法国评委和日本评委给出的平均分是90,日本评委和俄罗斯评委给出的平均分是92,那么中国评委和俄罗斯评委给出的平均分是_____。
A: 93分B: 94分C: 96分D: 98分
参考答案: C 本题解释:C【解析】设中、法、日、俄四国的评委给出的分数分别是A、B、C、D,根据题意可知:A+B=94×2,B+C=90×2,C+D=92×2,又因为A+D=(A+B)+(C+D)-(B+C)=94×2+92×2-90×2=(94+92-90)×2=96×2所以中国评委和俄国评委给出的平均分是96分,本题正确答案为C。
17、某单位2011年招聘了65名毕业生,拟分配到该单位的7个不同部门,假设行政部门分得的毕业生人数比其他部门都多,问行政部门分得的毕业生人数至少为多少名?_____
A: 10B: 11C: 12D: 13
参考答案: B 本题解释:正确答案是B考点趣味数学问题解析65÷7=9余2,即平均分配给7个不同部门还剩余2名毕业生,已知行政部门毕业生毕业生最多,所以只需将剩余的2名毕业生分配给行政部门即可(如果只分配1名,那么其他部门也会出现不少于10人的情况),可得9+2=11,故正确答案为B。
18、将一块三角形绿地沿一条直线分成两个区域,一块为三角形,一块为梯形,已知分出的三角形区域的面积为1.2亩,梯形区域的上、下底边分别为80米、240米,问分出的梯形区域的面积为多少亩?_____
A: 9.6B: 11.2C: 10.8D: 12.0
参考答案: A 本题解释:A。
19、连接正方体每个面的中心构成一个正八面体(如下图所示)。已知正方体的边长为6厘米,则正八面体的体积为_____立方厘米。
A: AB: BC: CD: D
参考答案: C 本题解释:正确答案是C考点几何问题解析 秒杀技该正八面体可看成上下两个正四棱锥组成,注意到每个四棱锥的底面面积为正方体底面面积的一半,每个四棱锥的高为立方体棱长的一半,因此可知每个四棱锥的体积为正方体体积的1/12,故该正八面体体积为正方体体积的1/6,于是其体积为1/6×6^3=36。
秒杀技该正八面体可看成上下两个正四棱锥组成,注意到每个四棱锥的底面面积为正方体底面面积的一半,每个四棱锥的高为立方体棱长的一半,因此可知每个四棱锥的体积为正方体体积的1/12,故该正八面体体积为正方体体积的1/6,于是其体积为1/6×6^3=36。
20、要使六位数15ABC6能被36整除,而且所得的商最小,那么这个六位数为:_____
A: 151236B: 152136C: 150156D: 151516
参考答案: C 本题解释:参考答案:C本题得分:题目详解:要求:1+5+6+A+B+C=9的倍数,得出A+B+C=610C+6能被4整除。得出C=3或者5,7,9结合上述两个,得出C=5,B=1,A=0,六位数为150156150156/36=4171考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除特征
21、某公司招聘甲、乙两种职位的人员共90人,甲、乙两种职位人员每月的工资分别为1500元和2500元,若甲职位的工资总支出是乙职位的40%,则乙职位招聘人数比甲职位多:_____
A: 24人B: 20人C: 18人D: 15人
参考答案: C 本题解释:【答案】C。解析:设甲职位有x人,则Z乙职位有(90-x)人。依题意有l500x=2500×(90-x)×40%,x=36人。因此乙职位有90-36=54人,比甲职位多54-36=18人。快速突破甲、乙职位的人均工资之比为1500:2500=3:5;甲职位的工资总支出是乙职位的40%,则甲、乙职位的总工资支出之比为40%:1=2:5,所以甲、乙职位的招聘人位之比为2/3:5/5=2:3,甲、乙共招聘90人,则乙职位招聘人数比甲职位多90×(3-2)/(3+2)=18人。
22、某礼堂的观众座椅共96张,分东、南、西三个区域摆放。现从东区搬出与南区同样多的座椅放倒南区,再从南区搬出与西区同样多的座椅放到西区,最后从西区搬出与东区剩下的座椅数量相同的座椅放到东区,这时三个区域的座椅数量相同。则最初南区的座椅有_____张。
A: 24B: 28C: 32D: 36
参考答案: B 本题解释:正确答案是B考点统筹规划问题解析第一次搬:东-南,2南,西;第二次搬:东-南,2南-西,2西;第三次搬:2东-2南,2南-西,2西-东+南。2东-2南=2南-西=2西-东+南,解得4南=7西,则南区座椅数肯定为7的倍数,只有B符合条件。故正确答案为B。标签数字特性
23、(2005广东下,第11题)要在一块边长为48米的正方形地里种树苗,已知每行相距3米,每竖列相距6米,四角各种一棵树,问一共可种多少棵树苗?_____
A: 128棵B: 132棵C: 153棵D: 157棵
参考答案: C 本题解释:参考答案:C题目详解:根据“每横行相距3米”、“四角各种一棵树”可知,应使用不封闭植树理论,且为两端均植树问题。两端均植树:点数=总长÷间距+1确定总长:48确定间距:3带入公式:点数=总长÷间距+1=48÷3+1=17根据“每竖列相距6米”,“四角各种一棵树”可知,应使用不封闭植树理论,且为两端均植树问题。两端均植树:点数=总长÷间距+1确定总长:48确定间距:6带入公式:点数=总长÷间距+1=48÷6+1=9总可种树:17×9=153棵。因此,选C。考查点:数量关系>数学运算>特殊情境问题>植树问题>两端均植树
24、某人在公共汽车上发现一个小偷向相反方向步行,10秒钟后他下车去追小偷,如果他的速度比小偷快一倍,比汽车慢4/5,则此人追上小偷需要_____。
A: 20秒B: 50秒C: 95秒D: 110秒
参考答案: D 本题解释:答案:D【解析】设某人速度为v,则小偷速为0.5v,汽车速为5v,10秒钟内,与小偷相差(0.5+5)v×10=55v,追求时速差为0.5v,所以所需时间为110秒。
25、某个月有五个星期六,已知这五个日期的和为85,则这个月中最后一个星期六是多少号?_____
A: 10B: 17C: 24D: 31
参考答案: D 本题解释:【答案】D。解析:一个月有五个星期六,日期和为85,则平均数为17,因为五个星期六的日期构成公差为7的等差数列,平均数即是第三个星期六的日期,则第五个星期六的日期为17+7+7=31,故正确答案为D。
26、(2006浙江,第35题)物美超市的收银台平均每小时有60名顾客前来排队付款,每一个收银台每小时能应付80名顾客付款。某天某时刻,超市如果只开设一个收银台,付款开始4小时就没有顾客排队了,问如果当时开设两个收银台,则付款开始几小时就没有顾客排队了?_____
A: 2小时B: 1.8小时C: 1.6小时D: 0.8小时
参考答案: D 本题解释:参考答案 题目详解:依题意:假设原有队伍的原有存量为
题目详解:依题意:假设原有队伍的原有存量为 ;每小时有60名顾客前来排队付款即自然增长速度为60;每小时收银台能应付80名顾客付款即消耗量为80;存量完全消失所耗用的时间3为所求,设为T;代入公式:
;每小时有60名顾客前来排队付款即自然增长速度为60;每小时收银台能应付80名顾客付款即消耗量为80;存量完全消失所耗用的时间3为所求,设为T;代入公式: 所以,选D。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
所以,选D。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
27、只装有动力桨的船,其单靠人工划船顺流而下的速度是水速的3倍。现该船靠人工划动从A地顺流到达B地,原路返回时只开足动力桨行驶,用时比来时少2/5。问船在静水中开足动力浆行驶的速度是人工划船速度的多少倍?_____
A: 2B: 3C: 4D: 5
参考答案: B 本题解释:正确答案是B考点行程问题解析设水速是1,则顺水速度为3,人工划船静水速度=3-1=2,顺水时间:逆水时间=1 1-2/5)=5:3,则顺水速度:逆水速度=3:5,所以逆水速度为5,动力浆静水速度=5+1=6,比例为6:2=3:1,故正确答案为B。标签赋值思想
1-2/5)=5:3,则顺水速度:逆水速度=3:5,所以逆水速度为5,动力浆静水速度=5+1=6,比例为6:2=3:1,故正确答案为B。标签赋值思想
28、两只蜗牛由于耐不住阳光照射,从井顶走向井底,白天往下走,一只蜗牛一个白天能走20厘米,另一只只能走15厘米;黑夜里往下滑,两只蜗牛下滑速度相同,结果一只蜗牛5昼夜到达井底,另一只却恰好用了6昼夜。问井深是多少厘米?_____
A: 150B: 180C: 200D: 250
参考答案: A 本题解释:A【解析】两只蜗牛白天路程差为20×5-15×6=10(厘米)。因为最终到达井底,所以蜗牛黑夜下滑的速度为每夜10÷(6-5)=10(厘米)。井深为(20+10)×5=150(厘米)。因此,正确答案为A。
29、把分数3/7用小数来表示,则小数点后第2008位的数字是_____。
A: 1B: 2C: 4D: 5
参考答案: D 本题解释:正确答案是D考点周期问题解析3/7=0.428571……循环节长度为6,而2008÷6=334……4,则第2008位数字与第4位数相同,即为”5”,故正确答案为D。
30、某单位邀请10为教师中的6为参加一个会议,其中甲,乙两位不能同时参加,则邀请的不同方法有_____种。
A: 84B: 98C: 112D: 140
参考答案: D 本题解释: 答案【D】解析:按要求:甲、乙不能同时参加分成以下几类:A.甲参加,乙不参加,那么从剩下的8位教师中选出5位,有C(8,5)=56种;B.乙参加,甲不参加,同(a)有56种;C.甲、乙都不参加,那么从剩下的8位教师中选出6位,有C(8,6)=28种。故共有56+56+28=140种。
31、一款手机打七折后价格为1050元,则该手机原价为_____元。
A: 1100B: 1400C: 1500D: 2100
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析原价为1050÷70%=1500,故正确答案为C。
32、某单位举办活动,需要制作8米长的横幅20条。用来制作横幅的原料有两种,一种每卷10米,售价10元;另一种每卷25米,售价23元。如果每卷原料截断后无法拼接,则该单位购买横幅原料最少需要花费_____元。
A: 146B: 158C: 161D: 200
参考答案: B 本题解释:正确答案是B考点统筹规划问题解析每卷10米的只能制作一条横幅,因此相当于单价为10元;每卷25米的只能制作三条条幅,因此相当于单价为23/3<10元。因此要制作20条横幅,购买方式为每卷25米的购买6卷,每卷10米的购买2卷,花费为23×6+10×2=158元。故正确答案为B。
33、一个长方形的周长是130厘米,如果它的宽增加  ,长减少
,长减少 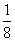 ,就得到一个相同周长的新长方形。原长方形的面积是多少?_____
,就得到一个相同周长的新长方形。原长方形的面积是多少?_____
A: 250平方厘米B: 400平方厘米C: 100 91EXAm.org00平方厘米D: 1000平方厘米
参考答案: D 本题解释:参考答案 题目详解:依题意可知:长的
题目详解:依题意可知:长的 和宽的
和宽的 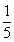 相等即长和宽的比是
相等即长和宽的比是 ;长方形的长、宽为:长=
;长方形的长、宽为:长= 厘米;宽=
厘米;宽= 厘米;原长方形的面积:
厘米;原长方形的面积: 平方厘米。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
平方厘米。考查点:数量关系>数学运算>几何问题>平面几何问题>周长与面积相关问题
34、已知a-b=46,a÷b÷c=2,a÷b-c=12,问a+b的值是_____。
A: 50B: 60C: 70D: 80
参考答案: A 本题解释:正确答案是A考点计算问题解析由a÷b÷c=2,a÷b-c=12,将a÷b看成一个整体,据此可求得:a÷b=24,c=12。又知a-b=46,联立可求得:a=48,b=2,因此a+b=50,故选择A选项。
35、王先生用清洗剂擦拭抽油烟机,已知每次可擦掉上次残留污垢的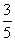 ,那么至少需要重复擦拭_____次,才能使最终残留的污垢不超过
,那么至少需要重复擦拭_____次,才能使最终残留的污垢不超过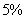 。
。
A: 4B: 5C: 3D: 2
参考答案: A 本题解释:参考答案:A题目详解:由题意可知:每次擦拭后残余的污垢为擦拭前的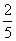 ;那么擦拭N次后:残留污垢是最初的
;那么擦拭N次后:残留污垢是最初的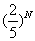 ;根据题意:列出不等式
;根据题意:列出不等式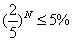 ,当
,当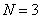 时,
时,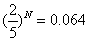 ,不符舍题意;即只有当
,不符舍题意;即只有当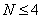 时,才能满足条件;因此至少要擦拭4次,才能使抽油烟机残留的污垢不超过
时,才能满足条件;因此至少要擦拭4次,才能使抽油烟机残留的污垢不超过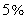 。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>不等式问题>由不等式确定未知量取值范围
。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>不等式问题>由不等式确定未知量取值范围
36、甲、乙两人在长30米的泳池内游泳,甲每分钟游37.5米,乙每分钟游52.5米,两人同时分别从泳池的两端出发,触壁后原路返回,如是往返。如果不计转向的时间,则从出发开始计算的1分50秒内两人共相遇了多少次?_____
A: 2B: 3C: 4D: 5
参考答案: B 本题解释:正确答案是B考点行程问题解析解析1:题目的关键在于第一次相遇,两人游过长度之和为泳池长,之后每次相遇,都需要两人再游过两个泳池长。两人一起游一个泳池长,所需时间为30÷(37.5+52.5)×60=20(秒),因此两人分别在20秒时、60秒时、100秒时相遇,共相遇3次。故正确答案为B。解析2:关键点同解析1。直接求出1分50秒两人合起来游过的距离为(37.5+52.5)×110÷60=165(米),为5.5个泳池长。而两人相遇时都恰是合起来游过距离为奇数个泳池长时,也即两人分别在合游1个、3个、5个泳池长时相遇,故共相遇3次。故正确答案为B。解析3:套用公式。先看迎面相遇,30×(2N-1)≤(37.5+52.5)×11/6,得N≤3.25,即有3次迎面相遇;再看追上相遇,30×(2N-1)≤(52.5-37.5)×11/6,得N≤23/24,即没有追及相遇。故总的相遇次数为3次。故正确答案为B。公式:两运动体从两端同时出发,相向而行,不断往返:第N次迎面相遇,两运动体路程和=全程×(2N-1);第N次追上相遇,两运动体路程差=全程×(2N-1)。标签公式应用
37、两个运输队,第一队有320人,第二队有280人,现因任务变动,要求第二队的人数是第一队人数的2倍,需从第一队抽调多少人到第二队?_____
A: 80人B: 100人C: 120人D: 140人
参考答案: C 本题解释:C设需抽调x人,根据题意可得2(320-x)=280+x,解得x=120人。
38、小明今年a岁,芳芳明年(a-4)岁,再过c年,他们相差_____。
A: 4岁B: c+4岁C: 5岁D: c-3岁
参考答案: C 本题解释:【解析】不管过多少年,两人年龄差永远不会改变;今年芳芳是a-5岁,所以相差5岁,选C。
39、某班学生不到50人,在一次考试中,有1/7人得优,1/3人得良,1/2人及格,其余的均不及格,那么不及格的人数是_____
A: 1 B: 2 C: 3 D: 4
参考答案: A 本题解释: A。通过题干可知,该班级最少人数应为7、3、2的最小公倍数,又因为不能超过50人,所以该班人数为7×3×2=42人。那么不及格的人数为42…61421=1。故正确答案为A。
40、一笔奖金分一等奖、二等奖和三等奖,每个一等奖的奖金是每个二等奖奖金的两倍,每个二等奖的奖金是每个三等奖奖金的两倍。如果评一、二、三等奖各两人,那么每个一等奖金是308元;如果评一个一等奖,三个三等奖,两个二等奖,那么一等奖的奖金是多少元_____
A: 154B: 196C: 392D: 490
参考答案: C 本题解释:【答案解析】①每个二等奖奖金为:308÷2=154(元)。②每个三等奖奖金为:154÷2=77(元)。③一共有奖金:(308+154+77)×2=1078(元)。④设一个三等奖奖金为x元,则一个二等奖奖金为2x元,一个一等奖奖金为4x元,列方程得:4x+4x+3x=1078,x=98。一等奖奖金为:98×4=392(元)。故正确答案为C。
41、_____ 
A: AB: BC: CD: D
参考答案: C 本题解释:正确答案是C考点行程问题解析
42、正四面体的棱长增长10%,则表面积增加_____
A: 21%B: 15%C: 44%D: 40%
参考答案: A 本题解释:参考答案:A题目详解:根据题意,可知:正四面体就是四个相等的正三角形。设原棱长a为1,则:原表面积为: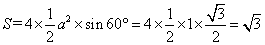 ;现表面积为:
;现表面积为: ;所以
;所以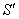 比S增加了:
比S增加了: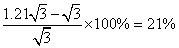 。所以,选A。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。所以,选A。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
43、两辆汽车同时从A、B两站相对开出,在B侧距中点20千米处两车相遇,继续以原速前进,到达对方出发站后又立即返回,两车再在距A站160千米处第二次相遇。求A、B两站距离是A_____。
A: 440千米B: 400千米C: 380千米D: 320千米
参考答案: A 本题解释:A[解析]首先,注意到第一次相遇后到第二次相遇时行的路程是出发到第一次相遇时行的路程的2倍。设A、B两站相距x千米,则第一次相遇时,B车行了(0.5x-20)千米;第二次相遇时,B车共行了(0.5x-20)×3(千米),或一个全长又160千米。列方程,得:(0.5x-20)×3=x+160x=440因此,本题正确答案为A。
44、甲、乙、丙三名运动员囊括了全部比赛项目的前三名,他们的总分分别是8、7和17分,甲得了一个第一名,已知各个比赛项目分数相同,且第一名的得分不低于二、三名得分的和,那么比赛共有多少个项目?_____
A: 3B: 4C: 5D: 6
参考答案: B 本题解释:【答案解析】全部比赛前三名的总分为8+7+17=32分,每个项目前三名的分数和至少是3+2+1=6分,所以每个项目前三名的分数和应该是32的大于6的约数,只能是8、16、32;如果是16或32,因为甲得了一个第一,所以甲的得分应大于8,不合题意,所以每个项目前三名的分数和是8分,共有项目32÷8=4个。
45、甲乙丙三人买书共花费96元钱,已知丙比甲多花16元,乙比甲多花8元,则甲、乙、丙花的钱的比是_____。
A: 3:5:4B: 4:5:6C: 2:3:4D: 3:4:5
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析乙和丙分别比甲多花8元和16元,因此三人共花的96元减去8元和16元即是甲花钱数的三倍,则甲花的钱数为(96-8-16)÷3=24元,乙花了32元,丙花了40元,三人之比为24:32:40=3:4:5,故正确答案为D。
46、某商品76件,出售给33位顾客,每位顾客最多买3件。买1件按原定价,买2件降价10%,买3件降价20%。最后结算,平均每件恰好按原价的85%出售,那么买3件的顾客有多少人?_____
A: 14B: 10C: 7D: 2
参考答案: A 本题解释:A【解析】 买2件商品按原价的90%,买3件商品按原价的80%。由于 =85%,即1个人买1件与1个人买3件的平均,每件正好是原定价的85%;又由于 =85%,所以2个人买3件与3个人买2件的平均,每件正好是原价的85%。因此,买3件的人数是买1件的人数与买2件人数的之和。设买2件的有x人,则买1件的有(33-x- x)÷2(人),买3件的有 x+(33-x- x)÷2(人)。因为共有商品76件,于是有方程(33-x- x)÷2+2x+3×[ x+(33-x- x)÷2]=76,解出x=15(人)。买3件的有x+(33-x- x)÷=14(人)故买3件的顾客有14人。选A。
47、从6名男生,5名女生中任选4人参加竞赛,要求男女至少各1名,有多少种不同的选法?_____
A: 240B: 310 C: 720 D: 1080
参考答案: B 本题解释: 答案【B】解析:此题从正面考虑的话情况比较多,如果采用间接法,男女至少各一人的反面就是分别只选男生或者女生,这样就可以变化成C(11,4)-C(6,4)-C(5,4)=310。
48、
49、有4支队伍进行4项比赛,每项比赛的第一、第二、第三、第四名分别得到5、3、2、1分。每队的4项比赛得分之和算作总分,如果已知各队的总分不相同,并且A队获得了三项比赛的第一名,问总分最少的队伍最多得多少分?_____
A: 7B: 8C: 9D: 10
参考答案: B 本题解释:正确答案是B考点抽屉原理问题解析设四个队分别为A、B、C、D,得分A>B>C>D。已知A得到3个第一,,要使D得到最多的分,那么A的得分要尽可能低,则第四项比赛得分为1,A总得分为5×3+1=16分;四项比赛总分为(5+3+2+1)×4=44,故剩余分数44-16=28;28÷3=9余1,则B最低得分为9+1=10,此时C、D同分,都为9分,不符合题意;则B最低得分为11,此时C得9分,D得8分,符合要求,得分情况如下:
A:5、5、5、1;B:3、3、3、2;C:1、1、2、5;D:2、2、1、3。故正确答案为B。
50、一个长方体的长、宽、高恰好是三个连续自然数,并且它的体积数值等于它的所有棱长之和的2倍,那么这个长方体的表面积为多少?_____
A: 74B: 148C: 150D: 154
参考答案: B 本题解释:参考答案:B题目详解:假设长方体的长、宽、高分别是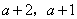 ,
,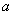 ,则:体积数值为:
,则:体积数值为: ,棱长之和的2倍为:
,棱长之和的2倍为: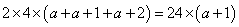 ,联立有:
,联立有: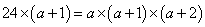 ,解得
,解得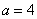 即长方体的长、宽、高分别为6,5,4,可见长方体的表面积为:
即长方体的长、宽、高分别为6,5,4,可见长方体的表面积为: 。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
51、两港相距560千米,甲船往返两港需105小时,逆流航行比顺流航行多用了35小时。乙船的静水速度是甲船的静水速度的2倍,那么乙船往返两港需要多少小时?_____
A: 24B: 20C: 28D: 48
参考答案: D 本题解释:参考答案:.D题目详解:甲船往返航行的时间分别是: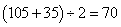 小时,70/2=35甲船逆水速度:
小时,70/2=35甲船逆水速度: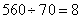 千米/小时,甲船顺水速度:
千米/小时,甲船顺水速度: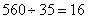 千米/小时,甲船在静水中的速度是:
千米/小时,甲船在静水中的速度是: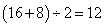 千米/小时,水流的速度是:
千米/小时,水流的速度是: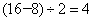 千米/小时;乙船在静水中的速度是:
千米/小时;乙船在静水中的速度是: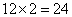 千米/小时,乙船往返一次所需要的时间是:
千米/小时,乙船往返一次所需要的时间是: 小时。所以,选D。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
小时。所以,选D。考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
52、某技校安排本届所有毕业生分别去甲、乙、丙3个不同的工厂实习。去甲厂实习的毕业生占毕业生总数的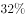 ,去乙厂实习的毕业生比甲厂少6人,且占毕业生总数的
,去乙厂实习的毕业生比甲厂少6人,且占毕业生总数的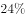 。问去丙厂实习的人数比去甲厂实习的人数:_____
。问去丙厂实习的人数比去甲厂实习的人数:_____
A: 少9人B: 多9人C: 少6人D: 多6人
参考答案: B 本题解释:正确答案是B,解析:根据题意去甲厂实习的人数占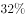 ,去乙厂实习的人数占
,去乙厂实习的人数占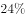 ,因此去丙厂实习的人数占
,因此去丙厂实习的人数占 ,故去丙厂的人数比去甲厂多
,故去丙厂的人数比去甲厂多 ;而去甲厂实习的人数比去乙厂的多
;而去甲厂实习的人数比去乙厂的多 ,为6人,故去丙厂的人数比去甲厂的应多
,为6人,故去丙厂的人数比去甲厂的应多 。故正确答案为B。考点:计算问题
。故正确答案为B。考点:计算问题
53、草地上插了若干根旗杆,已知旗杆的高度在1至5米之间,且任意两根旗杆的距离都不超过它们高度差的10倍。如果用一根绳子将所有旗杆都围进去,在不知旗杆数量和位置的情况下,最少需要准备多少米长的绳子?_____
A: 40B: 100C: 60D: 80
参考答案: D 本题解释:正确答案是D考点几何问题解析解析1: 解析2:旗杆最高为5米,最矮为1米。因此任意两旗杆间的距离不超过(5-1)×10=40米。以最矮的旗杆为原点,最矮的旗杆与最高的旗杆连线为x轴建立直角坐标系。当这两个旗杆间距最大时,如下左图所示。设其余任意旗杆高度为a。要满足与1米旗杆间距离不超过它们高度差的10倍,应在下图左边的圆范围内。要满足与5米旗杆间距离不超过它们高度差的10倍,应在下图右边的圆范围内。同时满足条件的旗杆只能位于两个旗杆的连线上。此时需要40×2=80米可把它们都围进去。若两个旗杆间距小于40米,如右图所示,其余旗杆应该在两圆相交的阴影范围内分布,此时需要2×[10(a-1)+10(5-a)]=80米。因此不论旗杆怎样分布,都需要至少80米长的绳子来保证把全部旗杆围进去,故正确答案为D。
解析2:旗杆最高为5米,最矮为1米。因此任意两旗杆间的距离不超过(5-1)×10=40米。以最矮的旗杆为原点,最矮的旗杆与最高的旗杆连线为x轴建立直角坐标系。当这两个旗杆间距最大时,如下左图所示。设其余任意旗杆高度为a。要满足与1米旗杆间距离不超过它们高度差的10倍,应在下图左边的圆范围内。要满足与5米旗杆间距离不超过它们高度差的10倍,应在下图右边的圆范围内。同时满足条件的旗杆只能位于两个旗杆的连线上。此时需要40×2=80米可把它们都围进去。若两个旗杆间距小于40米,如右图所示,其余旗杆应该在两圆相交的阴影范围内分布,此时需要2×[10(a-1)+10(5-a)]=80米。因此不论旗杆怎样分布,都需要至少80米长的绳子来保证把全部旗杆围进去,故正确答案为D。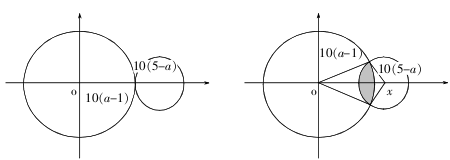 标签画图分析
标签画图分析
54、有34个偶数的平均数,如果保留一位小数点是15.9,如果保留两位小数,得数是_____?
A: 15.85B: 15.86C: 15.87D: 15.88
参考答案: D 本题解释:参考答案 题目详解:
题目详解: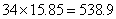
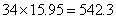 根据题意,34个数的总和应该能够被4整除,所以总和为:540
根据题意,34个数的总和应该能够被4整除,所以总和为:540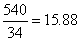 考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除的性质
考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除的性质
55、有两堆煤共重8.1吨,第一堆用掉2/3,第二堆用掉3/5,把两堆剩下的合在一起,比原来第一堆还少 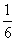 ,原来第一堆煤有多少吨?_____
,原来第一堆煤有多少吨?_____
A: 3.6B: 4.5C: 4D: 4.1
参考答案: A 本题解释:参考答案:A题目详解:解法一:根据题意,可知:用掉后,第一堆煤剩下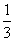 ,第二堆煤剩下
,第二堆煤剩下 ,两堆剩下的合在一起后,占原来第一堆的
,两堆剩下的合在一起后,占原来第一堆的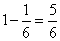 ,这其中有
,这其中有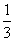 是原来第一堆剩下的,其余的
是原来第一堆剩下的,其余的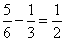 是原来第二堆剩下的,也就是说原来第二堆的
是原来第二堆剩下的,也就是说原来第二堆的 等于第一堆的
等于第一堆的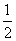 。所以原来第二堆的总数是原来第一堆的
。所以原来第二堆的总数是原来第一堆的 倍。所以原来第一堆煤有:
倍。所以原来第一堆煤有: 吨。所以,选A。解法二:如果第一堆用掉
吨。所以,选A。解法二:如果第一堆用掉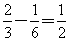 ,这用了的
,这用了的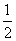 就和第二堆剩下的
就和第二堆剩下的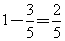 相等,所以,第二堆是第一堆的
相等,所以,第二堆是第一堆的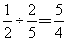 ,所以,第一堆煤有
,所以,第一堆煤有 吨。所以,选A。考查点:数量关系>数学运算>和差倍比问题>比例问题
吨。所以,选A。考查点:数量关系>数学运算>和差倍比问题>比例问题
56、某鞋业公司的旅游鞋加工车间要完成一出口订单,如果每天加工50 双,要比原计划晚3 天完成,如果每天加工60 双,则要比原计划提前2 天完成,这一订单共需要加工多少双旅游鞋?_____
A: 1200 双 B: 1300 双 C: 1400 双 D: 1500 双
参考答案: D 本题解释:【答案】D[解析]能被50、60整除的,排除B和C,再依次代入A和D,A不符合,所以选D。
57、2011×201+201100-201.1×2910的值为_____。
A: 20110B: 21010C: 21100D: 21110
参考答案: A 本题解释:正确答案是A考点计算问题解析原式=2011×201+2011×100-2011×291=2011×(201+100-291)=2011×10=20110。秒杀技原式中每一项都含有2011,因此结果必能被2011整除,只有A符合。标签数字特性
58、某公司举办年终晚宴,每桌安排7名普通员工与3名管理人员,到最后2桌时,由于管理人员已经安排完毕,便全部安排了普通员工,结果还是差2人才刚坐满,已经该公司普通员工数是管理人员的3倍,则该公司有管理人员_____名。
A: 24B: 27C: 33D: 36
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析设有管理人员的共有x桌,则管理人员共有3x人,从而普通员工共有9x人,则有9x=7x+18,解得x=9,所以管理人员共有27人。故正确答案为B。
59、(2009天津、湖北、陕西联考,第95题)有4支队伍进行4项体育比赛,每项比赛的第一、第二、第三、第四名分别得到5,3,2,1分,每队的4项比赛的得分之和算作总分,如果已知各队的总分不相同,并且A队获得了三项比赛的第一名,问总分最少的队伍最多得多少分?_____
A: 7B: 8C: 9D: 10
参考答案: B 本题解释:参考答案:B题目详解:本题需要运用“构造法”和“极端法”。由于题目求“总分最少的队伍最多得多少分”,我们需要让各队的得分尽可能的平均。每项比赛产生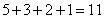 分,4项比赛一共产生
分,4项比赛一共产生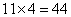 分,最终平均每人得到
分,最终平均每人得到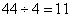 分。A已经获得了
分。A已经获得了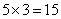 分,超过平均分,需要A最后=场比赛得尽量少的分,即1分,那么剩下3个人将得到
分,超过平均分,需要A最后=场比赛得尽量少的分,即1分,那么剩下3个人将得到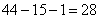 分。要让剩下三个人比分尽可能的平均,可以构造
分。要让剩下三个人比分尽可能的平均,可以构造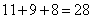 ,在这个条件下,部分最少的队伍可以得到最多的分数,即8分。下面我们构造这种比赛的情形:
,在这个条件下,部分最少的队伍可以得到最多的分数,即8分。下面我们构造这种比赛的情形: 考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛
考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛
60、有一食品店某天购进了6箱食品,分别装着饼干和面包,重量分别为8、9、16、20、22、27千克。该店当天只卖出1箱面包,在剩下的5箱中饼干的重量是面包的两倍,则当天食品店购进了_____千克面包。
A: 44B: 45C: 50D: 52
参考答案: D 本题解释:正确答案是D考点和差倍比问题解析由剩下的饼干重量是面包的两倍可知,剩下5箱的总重量一定能被3整除;6箱的总重量是8+9+16+20+22+27=102千克,也能被3整除,因此卖掉的一箱面包的重量也能被3整除,只能是9千克或27千克。若卖掉的一箱面包的重量是9千克,则剩下的面包重(102-9)÷3=31千克,剩余的各箱重量无法组合得到31。所以卖出的面包重27千克,剩余面包重(102-27)÷3=25千克。因此共购进了27+25=52千克面包,故正确答案为D。
61、(2008年江苏省公务员录用考试行测真题(A类))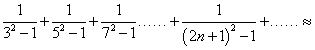 _____。
_____。
A: 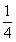 B: 1C:
B: 1C: 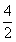 D: 无法计算
D: 无法计算
参考答案: A 本题解释:参考答案:A题目详解:应用消去法: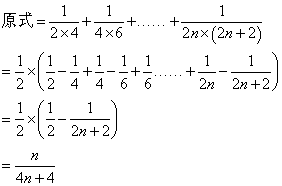 取极限之后其值为
取极限之后其值为 。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>消去法
。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>消去法
62、船在流速为每小时1000米左右的河上逆流而上,行至中午12点时,有一乘客的帽子落到了河里。乘客请求船家返回追赶帽子,这时船已经开到离帽子100米远的上游。已知在静水中这只船的船速为每分钟20米。假设不计调头的时间,马上开始追赶帽子,问追回帽子应该是几点几分?_____
A: 12点10分B: 12点15分C: l2点20分D: 12点30分
参考答案: A 本题解释:【解析】A。本题不需要考虑水速。船和帽子的相对速度为每分钟20米,距离相差100米,可得追上帽子需要5分钟;发现帽子到返回追帽子船走了100米,此段路程所花的时间为5分钟,则追回帽子应该是12点10分。
63、有一个上世纪80年代出生的人,如果他能活到80岁,那么有一年他的年龄的平方数正好等于那一年的年份。问此人生于哪一年?_____
A: 1980年B: 1983年C: 1986年D: 1989年
参考答案: A 本题解释:正确答案是A考点年龄问题解析根据题意可知该人年龄介于1980与2060之间,其中能满足年份数为平方数的仅2025年,2025=45×45,因此该人出生年份为2025-45=1980。故正确答案为A。
64、有甲、乙、丙、丁四个数,已知甲的8%为9,乙的9%为10,丙的10%为11,丁的11%为12,则甲、乙、丙、丁四个数中最小的数是_____。
A: 甲B: 乙C: 丙D: 丁
参考答案: D 本题解释:正确答案是D考点计算问题解析根据题意,甲=9÷0.08=100÷8+100,乙=10÷0.09=100÷9+100,丙=11÷0.10=100÷10+100,丁=12÷0.11=100÷11+100,不难发现丁数最小,故正确答案为D。
65、从一楼走到五楼,爬完一层休息30秒,一共要210秒,那么从一楼走到7楼,需要多少秒_____
A: 318B: 294C: 330D: 360
参考答案: C 本题解释:答案:C 解析:从一点走到五楼,休息了三次,那么每爬上一次需要的时间为(210-30×3)÷(5-1)=30秒,故从一楼走到七楼需要30×(7-1)+30×(7-2)=330秒。
66、小明和姐姐用2013年的台历做游戏,他们将12个月每一天的日历一一揭下,背面朝上放在一个盒子里,姐姐让小明一次性帮她柚出一张任意月份的30号或者31号。问小明一次至少应抽出多少张日历,才能保证满足姐姐的要求?_____
A: 346 B: 347 C: 348 D: 349
参考答案: C 本题解释:【答案】C。
67、甲乙两个工厂的平均技术人员比例为45%,其中甲厂的人数比乙厂多12.5%,技术人员的人数比乙厂的多25%,非技术人员人数比乙厂多6人。甲乙两厂共有多少人_____
A: 680B: 840C: 960D: 1020
参考答案: A 本题解释:【答案】A。解析:设甲厂技术人员有x,则乙厂有9x/8,两厂共有17x/8,即两厂总人数是17的倍数,选项中只有A、D符合。代入可知A符合题意。
68、河流赛道长120米,水流速度2米/秒,甲船速度为6米/秒,乙船速度为4米/秒。比赛进行两次往返,甲、乙同时从起点出发,先顺水航行,问多少秒后甲、乙船第二次迎面相遇?_____
A: 48B: 50C: 52D: 54
参考答案: C 本题解释:正确答案是C考点行程问题解析由于水速为2米/秒,所以顺行时候甲船速度是8米/秒,乙船速度是6米/秒。逆行时候甲船速度是4米/秒,乙船速度是2米/秒。甲乙的两次相遇分别在甲船第一次返回和甲船第二次顺行途中,甲第一次返回原地花费时间为120/8+120/4=45秒,此时乙到达对岸,逆水往回走,两船距离120-(4-2)×(45-120/6)=70米,再次相遇需要的时间为70÷(8+2)=7。所以总时间为45+7=52秒。故正确答案为C。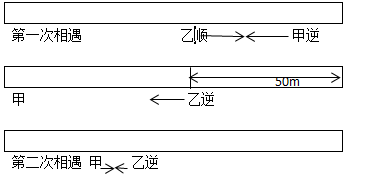
69、甲、乙、丙、丁四人共同投资一个项目,已知甲的投资额比乙、丙二人的投资额之和高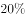 ,丙的投资额是丁的
,丙的投资额是丁的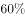 ,总投资额比项目的资金需求高
,总投资额比项目的资金需求高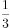 。后来丁因故临时撤资,剩下三人的投资额之和比项目的资金需求低
。后来丁因故临时撤资,剩下三人的投资额之和比项目的资金需求低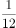 。则乙的投资额是项目资金需求的:_____
。则乙的投资额是项目资金需求的:_____
A: 1/6B: 1/5C: 1/4D: 1/3
参考答案: A 本题解释:正确答案是A,解析:根据条件,甲乙丙丁之和为 项目资金需求,甲乙丙之和为
项目资金需求,甲乙丙之和为 项目资金需求,故丁的投资额占项目需求的
项目资金需求,故丁的投资额占项目需求的 ;丙投资额是丁的
;丙投资额是丁的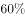 ,故丙投资额占
,故丙投资额占 ;
; ;
; ;联立方程可得
;联立方程可得 。故正确答案为A。考点:计算问题
。故正确答案为A。考点:计算问题
70、有20位运动员参加长跑,他们的参赛号码分别是1,2,3,……,20,至少要从中选出多少个参赛号码,才能保证至少有两个号码的差是13的倍数? _____
A: 12B: 15C: 14D: 13
参考答案: C 本题解释:答案:C 解析:将这20个数字分别为如下3组:(1,14),(2,15),(3,16),…,(7,20),8,9,10,11,12,13,考虑最差的情况,取出14个数字至少有2个数字在同一组,则它们之差为13。
71、甲、乙、丙三人,甲每分钟走50米,乙每分钟走40米,丙每分钟走35米,甲、乙从A地,丙从B地同时出发,相向而行,丙遇到甲2分钟后遇到乙,那么,A、B两地相距多少米?_____
A: 250米B: 500米C: 750米D: 1275米
参考答案: D 本题解释:正确答案是D考点行程问题解析设AB两地相距s米,丙遇到乙的时间为t,则丙遇到甲的时间为(t+2),由题意知s=(50+35)t,s=(40+35)(t+2),解得s=1275,故正确答案为D。公式:相遇问题,相遇距离=(大速度+小速度)×相遇时间。秒杀技甲、乙从A地,丙从B地同时出发,相向而行,所以甲丙相对速度为50+35=85米/分钟,乙丙相对速度为40+35=75米/分钟,所以AB两地距离能整除85和75,只有D项1275符合要求,故正确答案为D。标签数字特性公式应用
72、有一个周长为300米的封闭花坛,每3米挖坑栽树,挖了30个后,接到通知,以后改为每5米挖坑栽树,请问还需要挖多少个坑?_____
A: 40B: 42C: 43D: 45
参考答案: B 本题解释:参考答案:B题目详解:“在一个周长为300米的封闭花坛”,可知是只有一端植树问题。挖了30个坑,实际上是29个3米间距,即已经挖了的距离是:3×29=87米,剩下的距离是:300-29×3=213米。每5米挖一个坑,带入只有一端植树问题的公式:棵数=总长÷间距=213÷5=42…3因此42个坑还多出3米所以,选B。考查点:数量关系>数学运算>特殊情境问题>植树问题>只有一端植树
73、48与108的最大公约数是_____。
A: 6B: 8C: 24D: 12
参考答案: D 本题解释:正确答案是D考点倍数约数问题解析解析1:直接计算,得48与108的最大公约数为12。故正确答案为D。解析2:代入法,从大到小代入验证。故正确答案为D。标签最大公约数直接代入
74、某城市居民用水价格为:每户每月不超过5吨的部分按4元/吨收取,超过5吨不超过10吨的部分按6元/吨收取,超过10吨的部分按8元/吨收取。某户居民两个月共交水费108元,则该户居民这两个月用水总量最多为多少吨?_____
A: 21B: 24C: 17.25D: 21.33
参考答案: A 本题解释:正确答案是A考点分段计算问题解析在花费相同的情况下,要使两个月用水量最多,须使水价相对较便宜阶段的用水量最大,即两个月的“不超过5吨”和“5吨到10吨”部分的水量尽量多,通过计算2×(4×5+6×5)=100元,剩余180-100=8元,由于超出10吨的部分按8元/吨收取,故用水量为2×10+1=21吨。故正确答案为A。
75、现有边长1米的一个木质正方体,已知将其放入水里,将有0.6米浸入水中。如果将其分割成边长0.25米的小正方体,并将所有的小正方体都放入水中,直接和水接触的表面积总量为_____。
A: 3.4平方米B: 9.6平方米C: 13.6平方米D: 16平方米
参考答案: C 本题解释:正确答案是C考点几何问题解析 秒杀技对大正方体,易得其浸在水中的面积为3.4平方米,恰为选项A。而分解过小正方体后总浸水面积比为比值的倍数。故正确答案为C。
秒杀技对大正方体,易得其浸在水中的面积为3.4平方米,恰为选项A。而分解过小正方体后总浸水面积比为比值的倍数。故正确答案为C。
76、商场用9000元买进的手套全部出售后赚了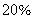 ,但是袜子卖得不好,只卖了9000元,赔了
,但是袜子卖得不好,只卖了9000元,赔了  。手套和袜子总体盈利多少?_____
。手套和袜子总体盈利多少?_____
A: 赔了600元B: 赔了700元C: 赚了800元D: 赚了900元
参考答案: C 本题解释:参考答案:C题目详解:手套卖了: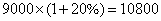 元;袜子成本为:
元;袜子成本为: 元;总收入与总成本相差:
元;总收入与总成本相差: 元;所以赚了800元。因此,选C。考查点:数量关系>数学运算>利润利率问题>成本、售价、利润、利润率之间的等量关系问题
元;所以赚了800元。因此,选C。考查点:数量关系>数学运算>利润利率问题>成本、售价、利润、利润率之间的等量关系问题
77、某城市居民用水价格为:每户每月不超过5吨的部分按4元/吨收取,超过5吨不超过10吨的部分按6元/吨收取,超过10吨的部分按8元/吨收取。某户居民两个月共交水费108元,则该户居民这两个月用水总量最多为多少吨?_____
A: 21B: 24C: 17.25D: 21.33
参考答案: A 本题解释:正确答案是A考点分段计算问题解析在花费相同的情况下,要使两个月用水量最多,须使水价相对较便宜阶段的用水量最大,即两个月的“不超过5吨”和“5吨到10吨”部分的水量尽量多,通过计算2×(4×5+6×5)=100元,剩余180-100=8元,由于超出10吨的部分按8元/吨收取,故用水量为2×10+1=21吨。故正确答案为A。
78、甲、乙二人2小时共加工54个零件,甲加工3小时的零件比乙加工4小时的零件还多4个。甲每小时加工多少个零件?_____
A: 11B: 16C: 22D: 32
参考答案: B 本题解释: 【解析】B。解法一、设俩人速度分别为x、y,则2x+2y=54,3x-4y=4,解得x=16;解法二、从第一句话知D不对。从第二句话中知甲每小时加工的零件是4的倍数。
79、河流赛道长120米,水流速度2米/秒,甲船速度为6米/秒,乙船速度为4米/秒。比赛进行两次往返,甲、乙同时从起点出发,先顺水航行,问多少秒后甲、乙船第二次迎面相遇?_____
A: 48B: 50C: 52D: 54
参考答案: C 本题解释:正确答案是C考点行程问题解析由于水速为2米/秒,所以顺行时候甲船速度是8米/秒,乙船速度是6米/秒。逆行时候甲船速度是4米/秒,乙船速度是2米/秒。甲乙的两次相遇分别在甲船第一次返回和甲船第二次顺行途中,甲第一次返回原地花费时间为120/8+120/4=45秒,此时乙到达对岸,逆水往回走,两船距离120-(4-2)×(45-120/6)=70米,再次相遇需要的时间为70÷(8+2)=7。所以总时间为45+7=52秒。故正确答案为C。
80、有11个人围成一个圆圈,依次编成1—11号,从1号起轮流表演节目,轮流的方法是:隔一个人表演一个节目,隔两个人表演一个节目,再隔一个人表演一个节目,隔两个人表演一个节目……这样轮流下去,至少要表演多少个节目,才能使每个人表演的次数同样?_____
A: 22B: 24C: 25D: 28
参考答案: A 本题解释:A【解析】本题考查的是周期问题。表演的人数共11人,且每个人表演次数相同,则至少要表演11N个节目。符合条件的只有A。
81、如果a,b均为质数,且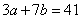 ,则如果a,b均为质数
,则如果a,b均为质数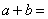 _____。
_____。
A: 5B: 6C: 7D: 8
参考答案: C 本题解释:参考答案:C题目详解:首先,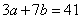 为奇数,根据数字的奇偶特性:中必有一个为偶数,一个为奇数;由于3、7为奇数,所以a与b必定也是一奇一偶;因此,
为奇数,根据数字的奇偶特性:中必有一个为偶数,一个为奇数;由于3、7为奇数,所以a与b必定也是一奇一偶;因此, 是奇数,排除B、D;其次,
是奇数,排除B、D;其次, 是奇数:则a,b中必有一个是质数中唯一的偶数
是奇数:则a,b中必有一个是质数中唯一的偶数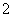 ;
;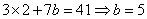 ,
, ;所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性
;所以,选C。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性
82、小强前三次的数学测验平均分是88分,要想平均分达到90分以上,他第四次测验至少要得多少分?_____
A: 98分B: 92分C: 93分D: 96分
参考答案: D 本题解释:【答案】D。解析:如果第四次测验后平均分数达到90分,则总分为90×4=360(分),第四次测验至少要360-88×3=96(分)。故正确答案为D。
83、小赵,小钱,小孙一起打羽毛球,每局两人比赛,另一人休息,三人约定每一局的输方下一局休息,结束时算了一下,小赵休息了2局,小钱共打了8局,小孙共打了5局,则参加第9局比赛的是:_____
A: 小钱和小孙B: 小赵和小钱C: 小赵和小孙D: 以上皆有可能
参考答案: B 本题解释:参考答案:B题目详解:小赵休息的2局即是小钱和小孙打了2局:则小钱和小赵打了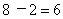 局;小孙和小赵打了
局;小孙和小赵打了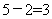 局:则一共打了
局:则一共打了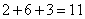 局;所以小孙11局中休息了6打了5局;由于不可能连续休息2局,所以小孙一定是休息1局打1局……;所以第9局小孙休息;小赵和小钱打;所以,选B。考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛
局;所以小孙11局中休息了6打了5局;由于不可能连续休息2局,所以小孙一定是休息1局打1局……;所以第9局小孙休息;小赵和小钱打;所以,选B。考查点:数量关系>数学运算>排列组合问题>比赛问题>循环赛
84、有一筐苹果,甲、乙、丙三人分,甲先拿了一半,乙拿了剩余的一半,丙再拿剩下的1/3,筐里还剩14个苹果。问:这一筐苹果有多少个?_____
A: 56B: 64C: 84D: 90
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析逆向考虑,丙拿剩下的1/3后还剩14个,说明丙拿之前有苹果14÷2/3=21个,则乙拿之前有21÷1/2=42个,甲拿之前有42÷1/2=84个,故正确答案为C。标签逆向考虑
85、某国家对居民收入实行下列税率方案;每人每月不超过3000美元的部分按照1%税率征收,超过3000美元不超过6000美元的部分按照X%税率征收,超过6000美元的部分按Y%税率征收(X,Y为整数)。假设该国某居民月收入为6500美元,支付了120美元所得税,则Y为多少_____
A: 6B: 3C: 5D: 4
参考答案: A 本题解释:A【解析】该国某居民月收入为6500美元要交的所得税为3000×1%+3000×X%+(6500-3000-3000)×Y%=120,化简为6X+Y=18,由于6X和18都能被6整除,因此Y也一定能被6整除分析选项,只有A符合。
86、地球表面的陆地面积和海洋面积之比是29︰71,其中陆地的四分之三在北半球,那么南、北半球海洋面积之比是_____
A: 284︰29B: 113︰55C: 371︰313D: 171︰113
参考答案: D 本题解释: 【解析】D。根据题干中的比例关系,可以推断出南、北半球的海洋面积之比为:
87、从钟表的12点整开始,时针与分针的第1次垂直与再一次重叠中间相隔的时间是:_____
A: 43分钟B: 45分钟C: 49分钟D: 61分钟
参考答案: C 本题解释:参考答案:C题目详解:分针1分钟走6度,时针1分钟走0.5度,分针与时针从第1次垂直到重叠时,分针比时针多走了270度,故所用时间为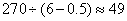 分钟。考查点:数量关系>数学运算>特殊情境问题>钟表问题>时针与分针的角度关系
分钟。考查点:数量关系>数学运算>特殊情境问题>钟表问题>时针与分针的角度关系
88、已知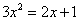 ,则
,则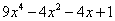 =_____ B: 1C: 2D: 4
=_____ B: 1C: 2D: 4
参考答案: C 本题解释:参考答案:C题目详解:根据题干中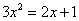 ,可得
,可得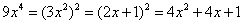 ,那么:
,那么: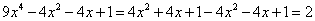 。因此,选C。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
。因此,选C。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
89、A大学的小李和B大学的小孙分别从自己学校同时出发,不断往返于A、B两校之间。现已知小李的速度为85米/分,小孙的速度为105米/分,且经过12分钟后两人第二次相遇。问A,B两校相距多少米?_____
A: 1140米B: 980米C: 840米D: 760米
参考答案: D 本题解释:易知到第二次相遇时,两人合起来走过的距离恰为A、B两校距离的3倍,因此A、B两校相距(85+105)×12÷3=760(米)。故选D。
90、13×99+135×999+1357×9999的值是_____。
A: 13507495B: 13574795C: 13704675D: 13704795
参考答案: D 本题解释:正确答案是D考点计算问题解析13×99+135×999+1357×9999=13×(100-1)+135×(1000-1)+1357×(10000-1)=﹙0.13+13.5+1357)×10000-(13+135+1357)=(1370.63-0.1505)×10000=13704795×10000,故正确答案为D。
91、一根木杆,第一次截去了全长的1/2,第二次截去所剩木杆的1/3,第三次截去所剩木杆的1/4,第四次截去所剩木杆的1/5,这时量得所剩木杆长为6厘米。问:木杆原来的长是多少厘米?_____
A: 15B: 26C: 30D: 60
参考答案: C 本题解释:C解析:6÷(1-1/5)÷(1-1/4)÷(1-1/3)÷(1-1/2)6÷(4/5×3/4×2/3×1/2)6÷1/5=30(厘米)故本题选C。
92、现有一个无限容积的空杯子,先加人1克酒精,再加入2克水,再加入3克酒精,再加人4克水,……,如此下去,问最终杯子中酒精溶液浓度为多少?_____ B: 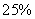 C:
C: 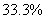 D:
D: 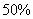
参考答案: D 本题解释:参考答案 题目详解:把加一次酒精和水看成一个流程:则经过
题目详解:把加一次酒精和水看成一个流程:则经过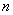 个流程后,杯子里面有
个流程后,杯子里面有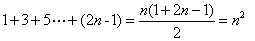 克酒精,而酒精溶液有:
克酒精,而酒精溶液有: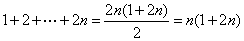 克。故此时酒精溶液浓度为:
克。故此时酒精溶液浓度为: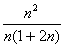 =
= ;当n趋于无穷大时,溶液浓度趋于
;当n趋于无穷大时,溶液浓度趋于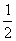 ,即
,即 。所以,选D。考查点:数量关系>数学运算>浓度问题>不同溶液混合
。所以,选D。考查点:数量关系>数学运算>浓度问题>不同溶液混合
93、甲、乙两船在相距90千米的河上航行,如果相向而行,3小时相遇,如果同向而行则15小时甲船追上乙船。求在静水中甲、乙两船的速度_____千米/小时。
A: 18,12B: 12,18C: 16,14D: 21,9
参考答案: A 本题解释:参考答案:.A题目详解:两船速度和:90/3=30千米/时两船速度差:90/15=6千米/时甲船 30+6)/2=18千米/时乙船:30-18=12千米/时考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
30+6)/2=18千米/时乙船:30-18=12千米/时考查点:数量关系>数学运算>行程问题>行船问题>基本行船问题
94、河道赛道长120米,水流速度为2米/秒,甲船速度为6米/秒,乙船速度为4米/秒。比赛进行两次往返,甲、乙同时从起点出发,先顺水航行,问多少秒后甲、乙船第二次迎面相遇?_____
A: 48 B: 50 C: 52 D: 54
参考答案: C 本题解释: C。
95、a大学的小李和b大学的小孙分别从自己学校同时出发,不断往返于a、b两校之间。现已知小李的速度为85米/分钟,小孙的速度为105米/分钟,且经过12分钟后两人第二次相遇。问a、b两校相距多少米?_____
A: 1140米B: 980米C: 840米D: 760米
参考答案: D 本题解释:【答案解析】设两校相距s米,则第二次相遇两人的路程和为3s米,有3s=(85+105)×12,解得s=760。
96、设“*”的运算法则如下:对任何若 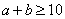 ,则
,则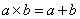 :若
:若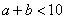 ,则
,则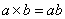 。则
。则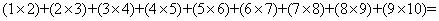 _____
_____
A: 125B: 115C: 105D: 120
参考答案: B 本题解释:参考答案:B题目详解:根据运算法则,根据题意:(1*2),(2*3),(3*4),(4*5)都满足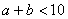 ,所以按计算
,所以按计算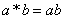 ;(5*6),(6*7),(7*8),(8*9),(9*10)都满足
;(5*6),(6*7),(7*8),(8*9),(9*10)都满足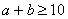 ,所以按
,所以按 计算;即:(1*2)+(2*3)+(3*4)+(4*5)+(5*6)+(6*7)+(7*8)+(8*9)+(9*10)=
计算;即:(1*2)+(2*3)+(3*4)+(4*5)+(5*6)+(6*7)+(7*8)+(8*9)+(9*10)=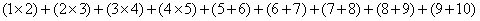 =
=
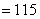 。所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
。所以,选B。考查点:数量关系>数学运算>计算问题之算式计算>定义新运算问题
97、共有20个玩具交给小王手工制作完成。规定,制作的玩具每合格一个得5元,不合格一个扣2元,未完成的不得不扣。最后小王共收到56元,那么他制作的玩具中,不合格的共有_____个。
A: 2B: 3C: 5D: 7
参考答案: A 本题解释:正确答案是A考点不定方程问题解析设小王制作合格玩具x个,不合格玩具y个,未完成的有z个。则x+y+z=20,5x-2y=56。为不定方程组,将选项代入验证,仅当y=2时,x与z有正整数解。故正确答案为A。
98、某日人民币外汇牌价如下表(货币单位:人民币元),按照这一汇率,100元人民币约可以兑换()美元。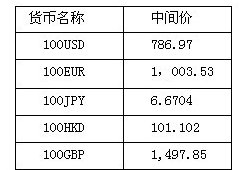
A: 12.61B: 12.66C: 12.71D: 12.76
参考答案: C 本题解释:【答案】C。解析:由表格,100美元=786.97人民币,则1美元=7.8697人民币,100人民币可以兑换为100÷7.8697≈10000÷787≈12.709≈12.71(美元),故正确答案为C。
99、甲、乙两种含金样品熔成合金,如甲的重量是乙的一半,得到含金68%的合金;如甲的重量是乙的3.5倍,得到含金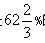 的合金。则乙的含金百分数为多少? _____
的合金。则乙的含金百分数为多少? _____
A: 72%B: 64%C: 60%D: 56%
参考答案: A 本题解释:【解析】A。解析:设甲的含金百分数为x,乙的含金百分数为y,可列方程x+2y=(1+2)×68%,3.5x+y=(1+3.5)× 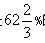 解得y=72%。
解得y=72%。
100、分数4/9、17/35、101/203、3/7、151/301中最大的一个是_____。
A: 4/9B: 17/35C: 101/203D: 151/301
参考答案: D 本题解释:正确答案是D考点其他解析4/9、17/35、101/203、3/7、151/301中只有151/301大于1/2,其他数字均小于1/2,因此151/301最大,故正确答案为D。