1、甲、乙两名运动员在400米的环形跑道上练习跑步,甲出发1分钟后乙同向出发,乙出发2分钟后第一次追上甲,又过了8分钟,乙第二次追上甲,此时乙比甲多跑了250米,问两人出发地相隔多少米:_____
A: 200B: 150C: 100D: 50
参考答案: B 本题解释:正确答案是B,解析方法一:设甲与乙的速度分别为 和
和 ,由题意,从第一次乙追上甲到第二次追及,甲与乙的路程差为400米,故
,由题意,从第一次乙追上甲到第二次追及,甲与乙的路程差为400米,故 ,解得两人速度差为
,解得两人速度差为 ,由于甲一共跑了11分钟,乙一共跑了10分钟,在后10分钟内,乙比甲多跑了
,由于甲一共跑了11分钟,乙一共跑了10分钟,在后10分钟内,乙比甲多跑了 ,由于乙最终比甲多跑250米,故甲最开始的1分钟跑了250米,又根据乙2分钟时第一次追上甲,可得该过程中甲与乙的路程差为
,由于乙最终比甲多跑250米,故甲最开始的1分钟跑了250米,又根据乙2分钟时第一次追上甲,可得该过程中甲与乙的路程差为 ,故两人最初相距
,故两人最初相距 。方法二:直接分析,在两人第一次相遇到第二次相遇的过程中,乙比甲多跑了400米,故在最开始的两分钟内甲比乙多跑150米,故两人开始时相距150米。故正确答案为B。考点:行程问题
。方法二:直接分析,在两人第一次相遇到第二次相遇的过程中,乙比甲多跑了400米,故在最开始的两分钟内甲比乙多跑150米,故两人开始时相距150米。故正确答案为B。考点:行程问题
2、今年某高校数学系毕业生为60名,其中70%是男生,男生中有1/3选择继续攻读硕士学位,女生选择攻读硕士学位的人数比例是男生选择攻读硕士学位人数比例的一半,那么该系选择攻读硕士学位的毕业生共有_____。
A: 15位B: 19位C: 17位D: 21位
参考答案: C 本题解释:正确答案是C考点和差倍比问题解析根据题意,毕业生中有30%是女生,攻读硕士学位的占1/6,因此该系攻读硕士学位的毕业生共有60×70%×1/3+60×30%×1/6=17位,故正确答案为C。
3、某彩票设有一等奖和二等奖,其玩法为从10个数字钟选出4个,如果当期开奖的4个数字组合与所选数字有3个相同则为二等奖,奖金为投注金额的3倍,4个数字完全相同则为一等奖,为了保证彩票理论中奖金额与投注金额之比符合国家50%的规定,则一等奖的奖金应为二等奖的多少倍?_____
A: 8B: 9C: 10D: 11
参考答案: D 本题解释:正确答案是D考点概率问题解析
4、一个工厂有若干个车间,为了调查产品的质量情况,采用简单随机抽样的方法,从全厂某天生产的3630件产品中抽取150件产品作样本进行质量检查。若第一车间这一天生产了440件产品,那么从该车间抽取的产品件数为_____。
A: 16B: 18C: 27D: 32
参考答案: B 本题解释:正确答案是B考点和差倍比问题解析
5、甲、乙两人沿直线从A地步行至B地,丙从B地步行至A地。已知甲、乙、丙三人同时出发,甲和丙相遇后5分钟,乙与丙相遇。如果甲、乙、丙三人的速度分别为85米/分钟、75米/分钟、65米/分钟。问A、B两地距离为多少米?_____
A: 8000米B: 8500米C: 10000米D: 10500米
参考答案: D 本题解释:正确答案是D考点行程问题解析本题理解的重点在于:在甲和丙相遇时,甲比乙多走的距离为后来乙丙一起走的距离。有了这个思想,就容易解出,甲和丙相遇时,甲比乙多走的距离为(75+65)×5=700m,假设甲和丙相遇的时候,甲走了a分钟,则(85-75)a=700,解得a=70。所以两地相距为(85+65)×70=10500米,故正确答案为D。
6、原计划用24个工人挖一定数量的土,按计划工作5天后,因为调走6人,于是剩下的工人每天比原计划多挖1方土才能如期完成任务,则原计划每人每天挖土_____。
A: 6方B: 5方C: 4方D: 3方
参考答案: D 本题解释:参考答案 题目详解:解法一:调走6人后,还剩下18人,每人每天增1方,则一天共增加18方,为这6个人的工作量,所以
题目详解:解法一:调走6人后,还剩下18人,每人每天增1方,则一天共增加18方,为这6个人的工作量,所以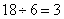 (方),因此,选D。解法二:设原计划每人每天挖土X方,调走人后每人每天挖土
(方),因此,选D。解法二:设原计划每人每天挖土X方,调走人后每人每天挖土 方,可列方程为:
方,可列方程为: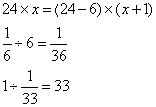
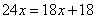
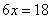
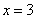 所以原计划每人每天挖土3方。因此,选D。考查点:数量关系>数学运算>工程问题>合作完工问题
所以原计划每人每天挖土3方。因此,选D。考查点:数量关系>数学运算>工程问题>合作完工问题
7、某单位订阅了30份学习材料发放给3个部门,每个部门至少发放9份材料。问一共有多少种不同的发放方法?_____
A: 7B: 9C: 10D: 12
参考答案: C 本题解释:正确答案是C考点排列组合问题解析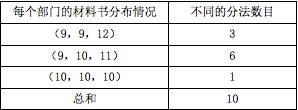 因此正确答案为C。
因此正确答案为C。
8、科学家对平海岛屿进行调查,他们先捕获30只麻雀进行标记,后放飞,再捕捉50只,其中有标记的有10只,则这一岛屿上的麻雀大约有多少只?_____
A: 150只B: 300只C: 500只D: 1 500只
参考答案: A
9、一段路程分为上坡、平路、下坡,三段路程长之比依次是1∶2∶3。小龙走各段路程所用时间之比依次是4∶5∶6。已知他上坡时速度为每小时3千米,路程全长是50千米,小龙走完全程用多少小时?_____
A: 10(5/12)B: 12C: 14(1/12)D: 10
参考答案: A
10、一件工程,甲单独完成需2天,乙单独完成需要4天,如果甲干完一天后,剩下的工程由乙单独完成,则干完此项工程共需_____。
A: 3天B: 4天C: 5天D: 6天
参考答案: A 本题解释:参考答案:A题目详解:解法一:设工作总量为“1”,那么:甲每天做的工作量为: ,乙每天做的工作量为:
,乙每天做的工作量为: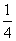 ,甲做1天后剩下的部分乙要做
,甲做1天后剩下的部分乙要做 天,则一共需
天,则一共需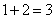 天。因此,选A。解法二:因为甲独干需两天,乙单独干需四天,现在甲干了乙干,则所需时间一定介于他俩单独干的天数之间,因此选A。(该解析由用户“你猜我是谁”于2011-03-0513:57:34贡献,感谢感谢!)考查点:数量关系>数学运算>工程问题>合作完工问题
天。因此,选A。解法二:因为甲独干需两天,乙单独干需四天,现在甲干了乙干,则所需时间一定介于他俩单独干的天数之间,因此选A。(该解析由用户“你猜我是谁”于2011-03-0513:57:34贡献,感谢感谢!)考查点:数量关系>数学运算>工程问题>合作完工问题
11、某商场开展购物优惠活动:一次购买300元及以下的商品九折优惠;一次购买超过300元的商品,其中300元九折优惠,超过300元的部分八折优惠。小王购物第一次付款144元,第二次又付款310元。如果他―次购买并付款,可以节省多少元?_____
A: 16B: 22.4C: 30.6D: 48
参考答案: A 本题解释:【解析】A。统筹优化问题。由题意,第一次付款144元可得商品原价为160元;第二次付款为310元可得原价为350元。故总价510元,按照优惠,需付款300×0.9+210×0.8=438(元),节省了454-438=16(元)。
12、(2009吉林)A、B两座城市距离:300千米,甲乙两人分别从A、B两座城市同一时间出发,已知甲和乙的速度都是50km/h,苍蝇的速度是100km/h,苍蝇和甲一起出发,然后遇到乙再飞回来,遇到甲再回去,直到甲乙相遇才停下来,请问苍蝇飞的距离是_____km?
A: 100B: 200C: 300D: 400
参考答案: C 本题解释:参考答案:C题目详解:根据题意,可知:甲乙相遇的时间为: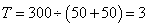 (小时),苍蝇飞行距离
(小时),苍蝇飞行距离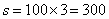 (千米)。所以,选C。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
(千米)。所以,选C。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线多次相遇问题
13、计算:(1+12)×(1-12)×(1+13)×(1-13)×…×(1+199)×(1-199)的值为_____。
A: 1C: 50/101D: 50/99
参考答案: D 本题解释:D[解析]原式=(1+1/2)×(1+1/3)×…×(1+1/99)×(1-1/2)×(1-1/3)×…×(1-1/99)=(3/2×4/3×5/4×…×99/98×100/99)×(1/2×2/3×3/4×…×97/98×98/99)=100/2×1/99=50/99因此,本题正确答案为D。
14、_____ 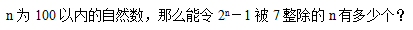
A: 32B: 33C: 34D: 35
参考答案: B 本题解释:正确答案是B考点余数与同余问题解析
15、地铁检修车沿地铁线路匀速前进,每6分钟有一列地铁从后面追上,每2分钟有一列地铁迎面开来。假设两个方向的发车间隔和列车速度相同,则发车间隔是_____。
A: 2分钟B: 3分钟C: 4分钟D: 5分钟
参考答案: B 本题解释:【答案】B。解析:此题为水速问题的变种,设两列地铁间的距离为1,则二者速度差为1/6,速度和为1/2,由水速问题的公式得,地铁的速度为(1/6+1/2)÷2=1/3,即3分钟发车一次。
16、某工厂有学徒工、熟练工、技师共80名,每天完成480件产品的任务。已知每天学徒工完成2件,熟练工完成6件,技师完成7件,且学徒工和熟练工完成的量相等,则该厂技师人数是熟练工人数的_____倍。
A: 6B: 8C: 10D: 12
参考答案: D 本题解释:列方程组。设学徒工、熟练工、技师分别有x,y,z名。则有:X+Y+Z=80,2X-96Y+7Z=48012X=6Y得到:X=15,y=5,Z=60,所以Z:Y=60:5=12。选D。
17、大洋百货商场十周年酬宾活动凡购买100元整商品的顾客可获得30元的现金返还。小李拿出1234元,最多可以买到多少元的商品?_____
A: 1324B: 1349C: 1694D: 1744
参考答案: D 本题解释:参考答案 题目详解:这个题目实质是酒瓶换酒的问题。100元现金=100元商品+30元现金,所以兑换标准是70元现金=100元商品,
题目详解:这个题目实质是酒瓶换酒的问题。100元现金=100元商品+30元现金,所以兑换标准是70元现金=100元商品,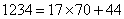 ,所以可以买到
,所以可以买到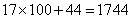 的商品。考查点:数量关系>数学运算>统筹问题>空瓶换酒问题
的商品。考查点:数量关系>数学运算>统筹问题>空瓶换酒问题
18、甲乙两队合挖一条水渠,甲队从东往西挖,乙队从西往东挖,甲队每天挖75米,比乙队每天多挖2.5米,两队合作8天后还差52米完工。这条水渠长多少米?_____
A: 1232B: 1323C: 1275D: 1352
参考答案: A 本题解释:正确答案是A考点工程问题解析水渠长度=8×75+8(75﹣2.5)+52=2×8×75﹣8×2.5﹢52=1200﹢52-20=1232(米)。故正确答案为A。
19、在平面直角坐标系中,如果点P(3a-9,1-a)在第三象限内,且横坐标纵坐标都是整数,则点P的坐标是_____。
A: (-1,-3)B: (-3,-1)C: (-3,2)D: (-2,-3)
参考答案: B 本题解释:正确答案是B考点计算问题解析根据点P在第三象限,有3a-9<0,1-a<0,得1
20、小华在练习自然数求和,从1开始,数着数着他发现自己重复数了一个数。在这种情况下,他将所数的全部数求平均,结果为7.4,请问他重复的那个数是_____。
A: 2B: 6C: 8D: 10
参考答案: B 本题解释:正确答案是B考点平均数问题解析 故正确答案为B。秒杀技总和=7.4×总个数,总和是整数,故总个数肯定是5的倍数。由于平均数是7.4,所以总个数应该是10或者15。如果总个数是10,总和应该是74,由于从1到10加起来才55,说明肯定不是10。总个数是15,总和应该是7.4×15=111,而从1到14加起来是(1+14)×14÷2=105,说明多加了一个6。故正确答案为B。标签数字特性
故正确答案为B。秒杀技总和=7.4×总个数,总和是整数,故总个数肯定是5的倍数。由于平均数是7.4,所以总个数应该是10或者15。如果总个数是10,总和应该是74,由于从1到10加起来才55,说明肯定不是10。总个数是15,总和应该是7.4×15=111,而从1到14加起来是(1+14)×14÷2=105,说明多加了一个6。故正确答案为B。标签数字特性
21、李大夫去山里给一位病人出诊,他下午1点离开诊所,先走了一段平路,然后爬上了半山腰,给那里的病人看病。半小时后,他沿原路下山回到诊所,下午3点半回到诊所。已知他在平路步行的速度是每小时4千米,上山每小时3千米,下山每小时6千米。请问:李大夫出诊共走了多少路?_____
A: 5千米B: 8千米C: 10千米D: l6千米
参考答案: B 本题解释: 
22、32头牛和若干匹马的价钱相等,如果把牛的头数和马的头数互换,马的头数再减少14头,此时二者的价钱又相等了。请问,每头牛和马的价格比为多少?_____
A: 2∶1 B: 3∶2 C: 4∶3 D: 3∶4
参考答案: D 本题解释:【答案】D。解析:设32头牛和x匹马的价钱相同,则交换后,x头牛和32-14=18头马的价钱相同,则32∶x=x∶18,解得x=24。故每头牛和马的价格比为24∶32=3∶4。
23、(2007浙江,第24题)林子里有猴子喜欢吃的野果,23只猴子可以在9周内吃光,21只猴子可以在12周内吃光,问如果有33只猴子-起吃,则需要几周吃光?(假定野果生长的速度不变)_____
A: 2周B: 3周C: 4周D: 5周
参考答案: C 本题解释:参考答案:C题目详解:依题意:设野果的原有存量为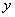 ;单位时间长出量即自然增长量为
;单位时间长出量即自然增长量为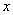 ,存量完全消失所消耗的时间
,存量完全消失所消耗的时间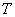 为所求;代入公式:
为所求;代入公式: 所以,选C。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
所以,选C。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
24、四人进行篮球传接球练习,要求每人接到球后再传给别人,开始由甲发球,并作为第一次传球。若第五次传球后,球又回到甲手中,则共有传球方式多少种:_____
A: 60;B: 65;C: 70;D: 75;
参考答案: A 本题解释:【答案解析】:选A,球第一次与第五次传到甲手中的传法有:C(1,3)×C(1,2)×C(1,2)×C(1,2)×C(1,1)=3×2×2×2×1=24,球第二次与第五次传到甲手中的传法有:C(1,3)×C(1,1)×C(1,3)×C(1,2)×C(1,1)=3×1×3×2×1=18,球第三次与第五次传到甲手中的传法有:C(1,3)×C(1,2)×C(1,1)×C(1,3)×C(1,1)=3×2×1×3×1=18,24+18+18=60种,具体而言:分三步:(1)在传球的过程中,甲没接到球,到第五次才回到甲手中,那有3×2×2×2=24种,第一次传球,甲可以传给其他3个人,第二次传球,不能传给自己,甲也没接到球,那就是只能传给其他2个人,同理,第三次传球和第四次也一样,有乘法原理得一共是3×2×2×2=24种。(2)因为有甲发球的,所以所以接下来考虑只能是第二次或第三次才有可能回到甲手中,并且第五次球才又回到甲手中。当第二次回到甲手中,而第五次又回到甲手中,故第四次是不能到甲的,只能分给其他2个人,同理可得3×1×3×2=18种。(3)同理,当第三次球回到甲手中,同理可得3×3×1×2=18种。最后可得24+18+18=60种
25、计算1/4+3/8+7/16+15/32+31/64+63/128+127/256+255/512+511/1024=?_____
A: 3×(513/1024)B: 3×(1023/1024)C: 4×(1/1024)D: 4×(511/1024)
参考答案: C 本题解释:【答案】C 解析∶原式=1/2-1/4+1/2-1-8+……+1/2-1/1024=4+1/1024=4×(1/1024)。
26、建造一个容积为8立方米,深为2米的长方体无盖水池。如果池底和池壁的造价分别为120元/平米和80元/平米,那么水池的最低总造价是_____元。
A: 1560B: 1660C: 1760D: 1860
参考答案: C 本题解释:正确答案是C考点几何问题解析本题考查几何等量最值性质。容积为8,深为2,则底面积为4,当底面为正方形时,周长最小,此时造价最低,故正方形边长为2,则底面周长为2×4=8,而侧面面积=深度×底面周长=2×8=16,则总造价=120×4+80×16=1760。故正确答案为C。标签几何等量最值性质
27、一个两位数等于其个位数字的平方与十位数字之和,这个两位数是_____。
A: 10B: 76C: 89D: 45
参考答案: C 本题解释:C
28、假设五个相异的正整数的平均数是15,中位数是18,则此五个相异的正整数中最大数的最大值可能是多少?_____
A: 24B: 32C: 35D: 42
参考答案: C 本题解释:五个数和为15×5=75,第三大的数是18。要让最大的数尽可能大,则其他数尽可能小。最小的两个数为1、2。第二大的数最小为19,所以最大的数的最大值为75-1-2-18-19=35。
29、某人在公共汽车上发现一个小偷向相反方向步行,10秒钟后他下车去追小偷,如果他的速度比小偷快一倍,比汽车慢4/5,则此人追上小偷需要_____。
A: 20秒B: 50秒C: 95秒D: 110秒
参考答案: D 本题解释:正确答案是D考点行程问题解析根据题中三者速度的比例关系,设此人、小偷和汽车的速度分别为2、1、10,10秒钟后此人下车时,与小偷的距离为10×(10+1)=110,与小偷的速度差为1,因此所需时间为110秒,故正确答案为D。
30、某儿童艺术培训中心有5名钢琴教师和6名拉丁舞教师,培训中心将所有的钢琴学员和拉丁舞学员共76人分剐平均地分给各个老师带领,刚好能够分完,且每位老师所带的学生数量都是质数。后来由于学生人数减少,培训中心只保留了4名钢琴教师和3名拉丁舞教师,但每名教师所带的学生数量不变,那么目前培训中心还剩下学员多少人?_____
A: 36B: 37C: 39D: 41
参考答案: D 本题解释:【答案】D。解析:假定每个钢琴教师带x个学生,每个拉丁舞教师带y个学生,则根据题意有:5x+6y=76。根据此方程,可知x必为偶数,而x与y均为质数,因此x=2,代回可得y=11。于是在学生人数减少后,还剩下学员为4×2+3×11=41个,故正确答案为D。
31、下列哪项能被11整除? _____
A: 937845678B: 235789453C: 436728839D: 867392267
参考答案: A 本题解释:A【解析】9+7+4+6+8=343+8+5+7=2334-23=11所以,答案是A。
32、一桶农药,加入一定量的水稀释后,浓度为15%;再加入同样多的水稀释,农药的浓度变为12%,若第三次再加入同样多的水,农药的浓度将变为多少?_____
A: 8%B: 10%C: 11%D: 13%
参考答案: B 本题解释:B。【解析】设δ加水稀释前农药量为x,?次所加水量为a,所求浓度为y%,则(x+a)15%=(x+2a)12%=(x+3a)y%,解得y%=10%。
33、某班共有49名学生,其中只有8个独生子女,又知其中28个有兄弟,25个有姐妹,则这个班级中有_____个人既有兄弟又有姐妹。
A: 2B: 8C: 12D: 20
参考答案: C 本题解释:正确答案是C考点容斥原理问题解析根据题干可知,非独生子女人数为49-8=41,设既有兄弟又有姐妹的人为x人,则41=(28-x)+(25-x)+x,解得x=12。故正确答案为C。秒杀技根据二集合容斥原理公式,可直接得到该人数=28+25-41=12,故正确答案为C。标签两集合容斥原理公式
34、
35、一公司销售部有4名区域销售经理,每人负责的区域数相同,每个区域都正好有两名销售经理负责,而任意两名销售经理负责的区域只有1个相同。问这4名销售经理总共负责多少个区域的业务?_____
A: 12B: 8C: 6D: 4
参考答案: C 本题解释:正确答案是C考点容斥原理问题解析由题意,每个区域正好有两名销售经理负责,可知2个经理一组对应一个区域;而根据,任意两名销售经理负责的区域只有1个相同,可知2个经理一组仅对应一个区域。由此两条可知,区域数其相当于从4个经理中任选2个有多少种组合,一种组合就对应一个区域,故共有6个区域。因此正确答案为C。
36、四人进行篮球传接球练习,要求每人接球后再传给别人。开始由甲发球,并作为第一次传球,若第五次传球后,球又回到甲手中,则共有传球方式_____。
A: 60种B: 65种C: 70种D: 75种
参考答案: A 本题解释:[解析]正确答案为A。细分一下传球路径,第一次接球的人只能是非甲,第二第三次接球的人可能是甲或非甲,第四次接球的人只能是非甲,第五次接球的人一定是甲,每次传球后接到球的人可分析如下:第一次第二次第三次第四次第五次第一种情况:非甲甲非甲非甲甲第二种情况:非甲非甲甲非甲甲第三种情况:非甲非甲非甲非甲甲按排列组合,第一种情况的传球方式有3×1×3×2×1=18,第二种有3×2×1×3×1=18,第三种情况有3×2×2×2×l=24,相加共有60种,故选A。
37、四个人夜间过一座独木桥,他们只有一个手电筒,一次同时最多可以有两人一起过桥,而过桥的时候必须有手电筒,所以就得有人把手电筒带来带去,两人同行时以较慢者的速度为准。四人过桥的时间分别是1分、2分、5分、l0分,他们过桥最少需要多少分钟?_____
A: 33B: 31C: 25D: 17
参考答案: D 本题解释:参考答案 题目详解:根据题意,要使得过桥时间最短,则应该保证过桥时间最长的两个人同时过去,但是由于有人把手电筒带来带去,因此,应该保证当这两个人过去后,在河对岸有一个用时比较短的人,把手电筒送回去,设过桥时间分别是l分、2分、5分、10分的人用A、B,C,D表示,可列表如下:
题目详解:根据题意,要使得过桥时间最短,则应该保证过桥时间最长的两个人同时过去,但是由于有人把手电筒带来带去,因此,应该保证当这两个人过去后,在河对岸有一个用时比较短的人,把手电筒送回去,设过桥时间分别是l分、2分、5分、10分的人用A、B,C,D表示,可列表如下: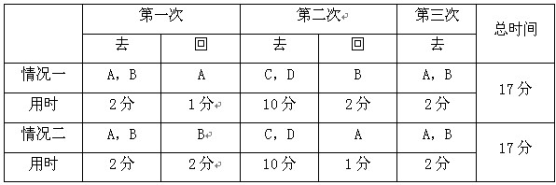 由表可知,答案为D。考查点:数量关系>数学运算>统筹问题>时间统筹问题
由表可知,答案为D。考查点:数量关系>数学运算>统筹问题>时间统筹问题
38、一份中学数学竞赛试卷共15题,答对一题得8分,答错一题或不做答均倒扣4分。有一个参赛学生得分为72,则这个学生答对的题目数是_____。
A: 9B: 10C: 11D: 12
参考答案: C 本题解释:参考答案:C题目详解:解法一:根据题意,设学生答对x题,则答错(15-x),可列方程: ,解得
,解得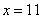 。解法二:学生答对一题得到8分,答错或不答损失
。解法二:学生答对一题得到8分,答错或不答损失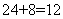 分;如果全部答对,将得到
分;如果全部答对,将得到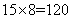 分;现在损失了
分;现在损失了 分,则学生答错
分,则学生答错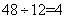 道,答对
道,答对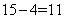 道。所以,选C。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>鸡兔同笼变形问题
道。所以,选C。考查点:数量关系>数学运算>特殊情境问题>鸡兔同笼问题>鸡兔同笼变形问题
39、有甲、乙两个足够大的杯子,甲盛水,乙盛纯果汁。先将甲杯的水倒进乙杯,使乙杯内液体增加一倍,调匀;再将乙杯的果汁倒进甲杯,使甲杯内液体增加一倍,调匀;……,如果倒三次。最后甲、乙两杯果汁的浓度各是_____。
A: 25%、37.5%B: 37.5%、50%C: 25%、25%D: 37.5%、25%
参考答案: A 本题解释:A。初始状态,甲的浓度为0,乙的浓度为100%;第一次操作后,甲的浓度为0,乙的浓度为50%;第二次操作后,甲的浓度为(0+50%)÷2=25%,乙的浓度为50%;第三次操作后,甲的浓度为25%,乙的浓度为(25%十50%)÷2=37.5%。
40、要折叠一批纸飞机,若甲单独折叠要半个小时完成,乙单独折叠需要45分钟完成,若两人一起折叠,需要多少分钟完成?_____
A: 10B: 15C: 16D: 18
参考答案: D 本题解释:答案:D【解析】此题实质上是一道工程问题。设纸飞机总量为1,则甲甲每分钟完成1/30,乙每分钟完成1/45,甲乙共花时间为1/(1/30+1/45)=18。故正确答案应为选项D。
41、一条线段中间另有6个点,则这8个点可以构成多少条线段?_____
A: 15B: 12C: 28D: 36
参考答案: C 本题解释:C。相邻两点构成线段8-1=7中间隔一点构成线段8-2=6类推距离最远两点(两端点)构成线段8-7=1,1+2+3+.+6+7=(1+7)*7/2=28选C
42、(2006浙江,第35题)物美超市的收银台平均每小时有60名顾客前来排队付款,每一个收银台每小时能应付80名顾客付款。某天某时刻,超市如果只开设一个收银台,付款开始4小时就没有顾客排队了,问如果当时开设两个收银台,则付款开始几小时就没有顾客排队了?_____
A: 2小时B: 1.8小时C: 1.6小时D: 0.8小时
参考答案: D 本题解释:参考答案 题目详解:依题意:假设原有队伍的原有存量为
题目详解:依题意:假设原有队伍的原有存量为 ;每小时有60名顾客前来排队付款即自然增长速度为60;每小时收银台能应付80名顾客付款即消耗量为80;存量完全消失所耗用的时间3为所求,设为T;代入公式:
;每小时有60名顾客前来排队付款即自然增长速度为60;每小时收银台能应付80名顾客付款即消耗量为80;存量完全消失所耗用的时间3为所求,设为T;代入公式: 所以,选D。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
所以,选D。考查点:数量关系>数学运算>特殊情境问题>牛儿吃草问题>标准型牛儿吃草问题
43、(2009.江苏C类)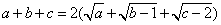 ,则
,则 =_____
=_____
A: 14B: 15C: 3D: 1
参考答案: A 本题解释:参考答案:A题目详解:转换等量关系: ,
,
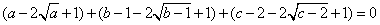
 运算:由于
运算:由于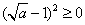 ,
,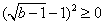 ,
,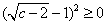 ,故
,故 ,
,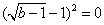 ,
, ,即
,即 ;因此,
;因此,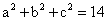 。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
。所以,选A。考查点:数量关系>数学运算>计算问题之算式计算>算式等式问题
44、A、B、C、D四支球队开展篮球比赛,每两个队之间都要比赛1场,已知A队已比赛了3场,B队已比赛了2场,C队已比赛了1场,D队已比赛了几场?()
A: 3B: 2C: 1
参考答案: B 本题解释:每个球队要比赛3场,则A队和B队、C队、D队各比赛1场,C队和A队比赛1场,B队和A队、D队各比赛1场,故D队比赛了2场。所以选B。
45、将棱长为1的正方体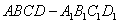 ,切去一角
,切去一角 后,剩下几何体的表面积是_____。
后,剩下几何体的表面积是_____。
A: 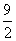 B: 5C:
B: 5C: 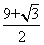 D:
D: 
参考答案: C 本题解释:参考答案:C题目详解:如右图所示,可知:原正方体表面积: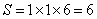 ;减少的表面积为:
;减少的表面积为: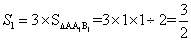 ;增加的表面积为:
;增加的表面积为: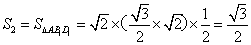 ;故剩下面积为:
;故剩下面积为: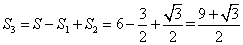 。所以,选C。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
。所以,选C。考查点:数量关系>数学运算>几何问题>立体几何问题>表面积与体积问题
46、一个四位数与7的和是没有重复数字的最小四位数,问原四位数的个位是多少?_____
A: 3B: 4C: 5D: 6
参考答案: D 本题解释:参考答案 题目详解:首先考虑没有重复数字的最小四位数:没有重复数字组成的最小四位数是1023;原四位数是:
题目详解:首先考虑没有重复数字的最小四位数:没有重复数字组成的最小四位数是1023;原四位数是: ;所以原四位数的个位是6。所以,选D。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
;所以原四位数的个位是6。所以,选D。考查点:数量关系>数学运算>计算问题之数的性质>数字问题>数字的拆分
47、某原料供应商对购买其原料的顾客实行如下优惠措施:①一次购买金额不超过1万元,不予优惠;②一次购买金额超过1万元,但不超过3万元,给九折优惠;③一次购买金额超过3万元,其中3万元九折优惠,超过3万元部分八折优惠。某厂因库容原因,第一次在该供应商处购买原料付款7800元,第二次购买付款26100元,如果他一次购买同样数量的原料,可以少付:_____
A: 1460元B: 1540元C: 3780元D: 4360元
参考答案: A 本题解释:【解析】A。第一次购买原料付款7800元,原料的总价值应为7800元,第二次购买时付款26100元,原料的总价值应为26100÷0.9=29000元。如果要将两次购买变成一次购买,则总价值应为7800+29000=36800元,而应该付款额为30000×0.9+6800×0.8=32440元,一次性购买比分两次购买可以节约7800+26100-32440=1460元。
48、超市规定每3个空汽水瓶可以换一瓶汽水,小李有11个空汽水瓶,最多可以换几瓶汽水?_____
A: 5瓶.B: 4瓶C: 3瓶D: 2瓶
参考答案: A 本题解释:A【精析】11个空汽水瓶可以换3瓶汽水余2个空瓶,3瓶汽水喝完之后一共余5个空汽水瓶,向超市借1瓶汽水,喝空之后退回6个空瓶,即再换2瓶汽水。因此3+2=5。
49、甲、乙两瓶中的混合液均是由柠檬汁、油和醋混合而成,其中甲瓶中混合液由柠檬汁、油和醋按1:2:3的体积比混合,乙瓶中混合液以3:4:5的体积比混合而成。现将两瓶中混合液混合在一起,得到体积比为3:5:7的混合液。则原来甲、乙两瓶溶液的体积比为_____。
A: 1:3B: 2:3C: 3:1D: 3:2
参考答案: D 本题解释:【答案】D。解析:
50、某年级组织一次春游,租船游湖,若每条船乘10人,则还有2人无座位;若每条船乘12人,则可少用一船,且人员刚好坐满,这时每人可节省5角钱。问租一条船需要多少钱?_____
A: 9元B: 24元C: 30元D: 36元
参考答案: D 本题解释:D【解析】 设船数为x,则10x+2=12(x-1),故x=7,所以人数为7×10+2=72,由“每人可节省5角钱”可得一条船的租金是72×5=360(角)=36(元)。
51、某单位《普法知识问答》的总平均分为87分,男同志的平均分为85分,女同志的平均分为90分,问此单位的男、女比例是多少?_____
A: 2/3B: 3/4 C: 3/2 D: 4/3
参考答案: C 本题解释:C。设女同志为1,男同志为 ,则(85x+90)÷(1+x)=87,解得x=3/2,即为男、女的比例,选C。
52、某网店连续3次下调某款手机的零售价格,每次下调幅度分别为:2.7%、5.5%和4.6%。经过3次调价,该款手机零售价较下调前大约下降了_____。
A: 12.3%B: 12.8%C: 13.3%D: 13.8%
参考答案: A 本题解释:正确答案是A考点经济利润问题解析连续调价三次以后价格为原价的(1-2.7%)×(1-5.5%)×(1-4.6%)>(1-2.7%-5.5%-4.6%),因此下降的价格幅度小于原价的2.7%+5.5%+4.6%=12.8%,故正确答案为A。
53、在一条公路旁有4个工厂,每个工厂的人数如图所示,且每两厂之间距离相等。现在要在公路旁设一个车站,使4个工厂的所有人员步行到车站总路程最少,这个车站应设在几号工厂门口?_____
A: 1号B: 2号C: 3号D: 4号
参考答案: C 本题解释:C【解析】 一般情况车站设在几个工厂的中间,即设在2号工厂或3号工厂门口。由于各厂人数不同,还是应通过计算再决定车站在哪一个工厂门口合适。如果设车站建在2号工厂门口,且设每两个工厂之间距离为1千米,那么4个工厂所有人员步行总路程为:1×100+1×80+2×215=100+80+430=610(千米)如果车站设在3号工厂门口,每两个工厂之间的距离为1千米,那么4个工厂所有人员步行总路程为:1×100×2+1×120+1×215=200+120+215=535(千米)显然,车站设在3号厂门口,才能使4个工厂所有人员步行到车站总路程最少。故本题选C。
54、某地收取手机费的标准是:每月打电话不超过30分钟,每分钟收费5角;如果超出30分钟,超出部分按每分钟7角收费。已知某月甲比乙多交了3元3角的手机费,则该月甲、乙两人共打了多少分钟电话?_____
A: 63B: 62C: 61D: 60
参考答案: A 本题解释:如果甲、乙两人打电话都超过30分钟,那么相差的电话费就应该是7的倍数,显然33不是7的倍数;如果甲、乙两人打电话都没超过30分钟,那么相差的电话费就应该是5的倍数,显然33不是5的倍数,因此只有一种情况:甲超过了30分钟,乙未达到30分钟。因为只有33=5×1+7×4一种情况满足题意,故甲打电话时间为30+4=34(分钟),乙打电话时间为30一1=29(分钟),甲、乙两人共打了34+29=63(分钟)。故选A。
55、学校五(一)班40名学生中,年龄最大的是13岁,最小的是11岁,那么其中至少有多少名学生是同年同月出生的?_____ B: 1C: 2D: 3
参考答案: C 本题解释:参考答案:C题目详解:解法一:把同年同月的放在一组里面,那么每一组可以作为1个“抽屉”;因此,可以构成3×12=36个“抽屉”,40÷36=1…4;由抽屉原理1可以得到,至少有2名学生是同年同月出生的。解法二:这40名同学的年龄最多相差36个月(三年),因40=1×36+4,故必有2人是同年、同月出生的。考查点:数量关系>数学运算>抽屉原理问题>抽屉原理1
56、某学校入学考试,确定了录取分数线。在报考的学生中,只有1/3被录取,录取者平均分比录取分数线高6分,没有被录取的学生其平均分比录取分数线低15分,所有考生的平均分是80分,推知录取分数线是_____。
A: 80B: 84C: 88D: 90
参考答案: C 本题解释:【答案】C。解析:不难看出,总共有多少人参加考试对本题的最终结果没有影响,仅是录取分数线的1/3对结果有影响,也即最后结果只与这个比例有关,而与总数无关。那么就可以直接看做录取了1个人,有2个人没录取,总人数为3人,则假定录取分数线为x分,于是得方程:(x﹢6)﹢(x-15)×2=80×3,解得x=88。故正确答案为C。
57、目前日期的流行记法是采用6位数字,即将公元年份的后两位数字记在最左边,中间两个数字表示月份,最末两位数字表示日份(例如1978年2月24日记为780224)。2010年1月22日应记为100122,这个六位数恰好能被66整除,因此这样的日期被称为“大顺日”,请问距2010年1月22日最近的一个大顺日是2010年的几月几日?_____
A: 2月21日B: 3月8日C: 3月20日D: 5月18日
参考答案: C 本题解释:参考答案:C本题得分:题目详解:根据题意:66=2×3×11,则依次考虑这个大顺日要分别能被2、3、11整除。能被2整除的数:末位数为0、2、4、6、8,排除A项;能被3整除的数:各位数字之和能被3(或9)整除,剩下三项都符合题意;能被11整除的数:奇数位数字之和与偶数位数字之和的差能被11整除;排除B;D项也能被66整除,但是不是距2010年1月22日最近的大顺日,因此只有C项符合题意,所以选C。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除特征
58、一串数排列成一行,它们的规律是这样的:前两个数都是1,从第三个数开始,每个数是它前两个数的和,也就是:1,1,2,3,5,8,13,21,34,…问:这串数的前100个数中有多少个偶数?_____
A: 33B: 32C: 50D: 39
参考答案: A 本题解释:参考答案:A题目详解:依题意:“1,1,2,3,5,8 ”根据“奇偶相加法则”:这个数列以“奇、奇、偶”为周期,循环出现;周期
”根据“奇偶相加法则”:这个数列以“奇、奇、偶”为周期,循环出现;周期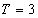 ;前99个数中有33个偶数:而第100个数是奇数。共33个偶数。所以,选A。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性
;前99个数中有33个偶数:而第100个数是奇数。共33个偶数。所以,选A。考查点:数量关系>数学运算>计算问题之数的性质>奇偶性与质合性问题>奇偶性
59、某商场举办羽绒服专卖会,一件羽绒服连续两次8折降价销售(即连续2次降价20%),降价后的价格为320元,问原价是多少?_____
A: 500B: 450C: 400D: 600
参考答案: A 本题解释:正确答案是A考点经济利润问题解析设原价为A元,连续两次降价20%后为0.8×0.8A=320,计算时采用分步计算而不计算0.8×0.8,易得A=500,故正确答案为A。
60、某市夏季高峰期对居民用电采用如下办法收取电费:用户月用电量在50度以内的部分,按0.4元/度收费;超过50度的部分,按0.8元/度收费。该市一户居民去年夏季高峰期有一个月的电费为32元,那么这个月该用户用电度数是_____。
A: 50度B: 55度C: 60度D: 65度
参考答案: D
61、一本100多页的书,被人撕掉了4张,剩下的页码总和为8037,则该书最多有多少页?_____
A: 134B: 136C: 138D: 140
参考答案: A 本题解释:【答案】A。解析:撕掉一张纸,其正反两面的两个页码之和为奇数,则撕掉4张,页码总数必为偶数,剩余页码和为8037,所以原书的页码总和必然为奇数,由此排除BD(BD选项能被4整除,而连续4页的页码和必然为偶数)。代入C,可知整书的页码总和为(1+138)÷2×138=9591,于是撕掉的页码和为9591-8037=1554,那么撕掉的8页的页码平均值为194.25,显然与最多138页矛盾。故正确答案为A。
62、有一只怪钟,每昼夜设计成10小时,每小时100分钟,当这只怪钟显示5点时,实际上是中午12点,当这只怪钟显示8点50分时,实际上是_____。
A: 17点50分B: 18点10分C: 20点04分D: 20点24分
参考答案: D 本题解释:正确答案是D考点钟表问题解析怪钟从5点走到8点50经过了3×100+50=350分钟,又因为怪钟每天为1000分钟,正常钟为1440分钟,设正常钟走过了X分钟,则有350/1000=X/1440,解得X=504,从12点开始经过了504分钟,时间为20时24分。故正确答案为D。
63、如图所示,△ABC是直角形,四边形IBFD和四边形HFGE都是正方形,已知AI=1cm,IB=4cm,正方形HFGE的面积是_____。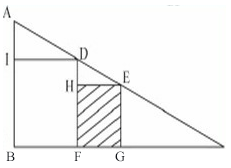
A: AB: BC: CD: D
参考答案: C 本题解释:正确答案是C考点几何问题解析设正方形HFGE的边长为X,由三角形EHD相似于三角形DIA可知,EH/DH=DI/DA,即X/(4-X)=4/1,解得X=16/5,那么正方形面积为16/5×16/5=10.24,故正确答案为C。
64、甲、乙、丙三种货物,如果购买甲3件、乙7件、丙1件需花3.15元,如果购买甲4件、乙10件、丙1件需花4.2元,那么购买甲、乙、丙各1件需花多少钱?_____
A: 1.05B: 1.4C: 1.85D: 2.1
参考答案: A 本题解释:正确答案是A考点不定方程问题解析甲×3+乙×7+丙×1=3.15……①甲×4+乙×10+丙×1=4.20……②这是不定方程组,无法解得每个未知数的具体值。换言之,未知数的解存在无穷多个,而题目中四个选项均为确定数值,所以未知数的具体值为多少并不影响甲+乙+丙的值,也即只需要求出其中一组解即可。对此,可以设定最复杂的那个为0,即乙=0,代入后解二元一次方程组,解得甲=1.05,丙=0,即可得甲+乙+丙=1.05。故正确答案为A。秒杀技①×3-②×2可得:甲+乙+丙=3.15×3-4.20×2=1.05。故正确答案为A。
65、某工厂有一大型储水罐供全厂生产用水,已知每天晚8点至早8点蓄水,蓄水管流量为8吨/小时,工厂用水为每天早8点至晚12点,用量为6吨/时,储水罐中水位最高时的储水量至少是_____。
A: 48吨B: 72吨C: 84吨D: 96吨
参考答案: B 本题解释:B【解析】从每晚8点开始蓄水,至早8点水位一直在升高,在这之后,蓄水停止,水位下降;晚8点至晚12点之间,水位上升,但同时仍在用水。故水位最高点应为早8点。8×(12一4)+4×(8一6)=72(吨)。
66、三名工人师傅李群、张强和王充分别加工200个零件,他们同时开始工作,当李群加工200个零件的任务全部完成时,张强才加工了160个,王充还有48个没有加工。当张强加工200个零件的任务全部完成时,王充还有_____个零件没有加工。
A: 15B: 25C: 9D: 10
参考答案: D 本题解释:正确答案是D考点工程问题解析张强加工160个零件时,王充加工了200-48=152个,即张强和王充的效率比为160:152=20:19,设张强加工200个零件时王充加工了x个,根据题意有x:200=19:20,解得x=190,即还有10个没有加工,故正确答案为D。
67、三个连续的偶数的乘积为192,那么其中最大的数是多少?_____
A: 4B: 6C: 12D: 8
参考答案: D 本题解释:答案:D【解析】设最小的偶数为x,则这三个偶数依次为x,x+2,x+4,故x?(x+2)?(x+4)=192。用代入法解答。经过验证x=4,则最大的偶数为8。因此正确答案为D。
68、如果两个四位数的差等于8921,那么就说这两个四位数组成一个数对,问这样的数对共有多少个?_____
A: 80B: 79C: 83D: 81
参考答案: B 本题解释:【解析】从两个极端来考虑这个问题:最大为9999-1078=8921,最小为9921-1000=8921,所以共有9999-9921+1=79个,或1078-1000+1=79个。故应选择B。
69、如下图,梯形ABCD的对角线AC⊥BD,其中AD=1/2,BC=3,AC=2×4/5,BD=2.1。问梯形ABCD的高AE的值是_____。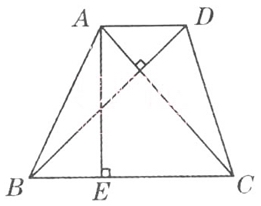
A: 43/24B: 1.72C: 4/252D: 1.81
参考答案: C 本题解释:【解析】由AC×BD=(AD+BC)×AE→AE=42/25。
70、有浓度为 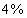 的盐水若干克,蒸发了一些水分后浓度变成
的盐水若干克,蒸发了一些水分后浓度变成 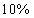 ,再加入300克
,再加入300克 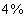 的盐水后.浓度变为
的盐水后.浓度变为 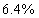 的盐水,问最初的盐水多少克?_____
的盐水,问最初的盐水多少克?_____
A: 200B: 300C: 400D: 500
参考答案: D 本题解释:参考答案 题目详解:解法一:应用十字交叉法:根据题意,设10%的盐水的质量为
题目详解:解法一:应用十字交叉法:根据题意,设10%的盐水的质量为 克,则有
克,则有 ,故有
,故有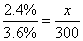 ,解得
,解得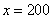 。则原有的盐水质量为
。则原有的盐水质量为 ,所以,选D。解法二:应用方程法:设最初的盐水为
,所以,选D。解法二:应用方程法:设最初的盐水为 克,300克4%的盐水含盐12克,则可以列方程为:
克,300克4%的盐水含盐12克,则可以列方程为: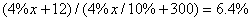 其中:
其中: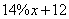 为盐水混合后的盐含量;
为盐水混合后的盐含量; 为盐水混合后的盐水质量;解得,
为盐水混合后的盐水质量;解得,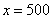 克所以,选D。考查点:数量关系>数学运算>浓度问题>不同溶液混合
克所以,选D。考查点:数量关系>数学运算>浓度问题>不同溶液混合
71、将一批电脑装车,装了28车时,还剩80%没有装,装了85车时,还剩1320台没有装。这批电脑共有多少台?_____
A: 3360B: 3258C: 2752D: 280 0
参考答案: A 本题解释:这批电脑总共可以装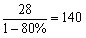 辆车,每辆车可以装
辆车,每辆车可以装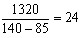 台电脑,所以一共有
台电脑,所以一共有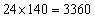 台电脑。
台电脑。
72、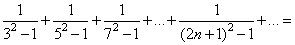 _____
_____
A: 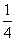 B: 1C:
B: 1C: 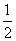 D: 无法计算
D: 无法计算
参考答案: A 本题解释:参考答案:A题目详解:前n项和为: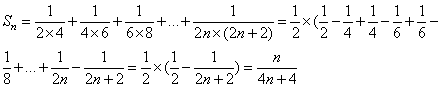 故其极限为
故其极限为 考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>分式数列求和
73、火车驶过长900米的铁路桥,从车头上桥到车尾离桥共用1分25秒,紧接着列车又穿过一条长1800米的隧道,从车头进隧道到车尾离开隧道用了2分40秒,则火车车身长为_____。
A: 120米B: 100米C: 80米D: 90米
参考答案: A 本题解释:参考答案:A题目详解:应用方程法:由于火车速度相同,设车身长度为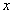 米;从车头上桥到车尾离桥火车行驶距离为:
米;从车头上桥到车尾离桥火车行驶距离为: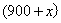 米;从车头进遂道到车尾离开遂道行驶距离为:
米;从车头进遂道到车尾离开遂道行驶距离为: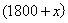 米;列方程:
米;列方程: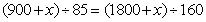 ,解
,解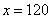 米。所以,选A。考查点:数量关系>数学运算>行程问题>初等行程问题
米。所以,选A。考查点:数量关系>数学运算>行程问题>初等行程问题
74、甲对乙说:当我的岁数是你现在岁数时,你才4岁。乙对甲说:当我的岁数到你现在岁数时,你将有67岁。甲乙现在各有_____。
A: 45岁,26岁B: 46岁,25岁C: 47岁,24岁D: 48岁,23岁
参考答案: B 本题解释:正确答案是B考点年龄问题解析
75、(2008陕西,第20题)某个月有五个星期六,已知这五个日期之和为85,则这个月最后一个星期六是多少号?_____
A: 10B: 17C: 24D: 31
参考答案: D 本题解释:参考答案 题目详解:五个日期之和为85:平均数(即“中位数”)应该是
题目详解:五个日期之和为85:平均数(即“中位数”)应该是 ,因此5个数正中间那个为17;这5个日期(相差7)分别为:3、10、17、24、31;最后一个星期六是31号;所以,选D。考查点:数量关系>数学运算>特殊情境问题>日期星期问题
,因此5个数正中间那个为17;这5个日期(相差7)分别为:3、10、17、24、31;最后一个星期六是31号;所以,选D。考查点:数量关系>数学运算>特殊情境问题>日期星期问题
76、某商品按定价的80%(八折)出售,仍能获得20%的利润,问定价时期望的利润率是多少?_____
A: 50%B: 40%C: 30%D: 20%
参考答案: A 本题解释:正确答案是A考点经济利润问题解析设定价为y,成本为x,由题意得0.8y-x=0.2x,则y=1.5x,定价时期望的利润率为(y-x)÷x=50%,故正确答案为A。
77、甲乙两个工厂的平均技术人员比例为45%,其中甲厂的人数比乙厂多12.5%,技术人员的人数比乙厂的多25%,非技术人员人数比乙厂多6人。甲乙两厂共有多少人_____
A: 680B: 840C: 960D: 1020
参考答案: A 本题解释:【答案】A。解析:设甲厂技术人员有x,则乙厂有9x/8,两厂共有17x/8,即两厂总人数是17的倍数,选项中只有A、D符合。代入可知A符合题意。
78、袋中有7只白球,3只红球,白球中有4只木球,3只塑料球;红球中有2只木球,1只塑料球。现从袋中任取1球,并且每只球被取到的可能性相同。若已知取到的球是白球,问它是木球的概率是多少?_____
A: 4/7B: 7/25C: 2/25D: 2/5
参考答案: A 本题解释:参考答案:A题目详解:取到白球中的木球的概率: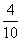 ;取到白球的概率为:
;取到白球的概率为: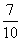 ;根据条件概率公式:
;根据条件概率公式: ;所以,选A。考查点:数量关系>数学运算>概率问题>条件概率
;所以,选A。考查点:数量关系>数学运算>概率问题>条件概率
79、药厂使用电动研磨器将一批晒干的中药磨成药粉。厂长决定从上午10点开始,增加若干台手动研磨器进行辅助作业。他估算如果增加2台,可在晚上8点完成,如果增加8台,可在下午6点完成。问如果希望在下午3点完成,需要增加多少台手工研磨器?_____
A: 20B: 24C: 26D: 32
参考答案: C 本题解释:【答案】C。解析:设原有电动研磨器为N台,需要增X台手工研磨器,根据牛吃草公式有:Y=(N+2)10;Y=(N+8)8,解得N=22,Y=240;代入Y=(N+X)5解得X=26,故选择C选项。
80、某外语班的30名学生中,有8人学习英语,12人学习日语,3人既学英语也学日语,问有多少人既不学英语又没学日语?_____
A: 12B: 13C: 14D: 15
参考答案: B 本题解释:正确答案是B考点容斥原理问题解析
81、从一楼走到五楼,爬完一层休息30秒,一共要210秒,那么从一楼走到7楼,需要多少秒_____
A: 318B: 294C: 330D: 360
参考答案: C 本题解释:答案:C 解析:从一点走到五楼,休息了三次,那么每爬上一次需要的时间为(210-30×3)÷(5-1)=30秒,故从一楼走到七楼需要30×(7-1)+30×(7-2)=330秒。
82、今年小方父亲的年龄是小方的3倍,去年小方的父亲比小方大26岁,那么小方明年多大?_____
A: 16B: 13C: 15D: 14
参考答案: D 本题解释:D【解析】设今年小方的年龄为,则小方的※亲的年龄为3,由此可得方程:x-1=3x-1-26,解得x=13,故小方明年的年龄为13+1=14(岁)。故正确答案为D。
83、(2009山东,第119题)某工程项目由甲项目公司单独做需4天完成,由乙项目公司单独做需6天才能完成,甲、乙、丙三个公司共同做2天就可以完成,现因交工日期在即,需多公司合作,但甲公司因故退出,则由乙、丙公司合作完成共需多少天?_____
A: 3B: 4C: 5D: 6
参考答案: B 本题解释:参考答案:B题目详解:假设工程总量为“12”,由题意易知:甲的效率为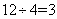 ,乙的效率为
,乙的效率为 ,甲、乙、丙的效率和为
,甲、乙、丙的效率和为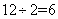 ,从而我们知道丙的效率为
,从而我们知道丙的效率为 。因此,乙、丙合作完成需要
。因此,乙、丙合作完成需要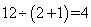 (天)。因此,选B。考查点:数量关系>数学运算>工程问题>合作完工问题
(天)。因此,选B。考查点:数量关系>数学运算>工程问题>合作完工问题
84、王方将5万元存入银行,银行利息为1.5%/年,请问2年后,它的利息是多少?_____
A: 1500元B: 1510元C: 1511元D: 1521元
参考答案: C 本题解释:正确答案是C考点经济利润问题解析根据题意两年后利息为50000×(1+0.015)×(1+0.015)-50000=2×50000×0.015+50000×0.015×0.015=1511.25,故正确答案为C。
85、松鼠妈妈采松果,晴天每天可采20个,雨天每天只能采12个。它一连几天共采了112个松果,平均每天采14个。这几天中有几天下雨?_____
A: 3B: 4C: 5D: 6
参考答案: D 本题解释:【答案解析】松鼠妈妈一连采了松果的天数为:112÷14=8(天)。设雨天有x天,则晴天有(8-x)天,列方程得20×(8-x)+12x=1125×(8-x)+3x=28x=6故本题正确答案为D。
86、在同一环形跑道上小陈比小王跑得慢,两人都按同一方向跑步锻炼时,每隔12分钟相遇一次;若两人速度不变,其中一人按相反方向跑步,则隔4分钟相遇一次。问两人跑完一圈花费的时间小陈比小王多几分钟?_____
A: 5B: 6C: 7D: 8
参考答案: B 本题解释:不妨设小王和小陈速度分别为x,y,跑道长度为s,则:两人都按同一方向跑步锻炼时,每隔12分钟相遇一次,说明s/(x—y)=12;若两人速度不变,其中一人按相反方向跑步,则每隔4分钟相遇一次,说明s/(x+y)=4;解得s=6x=12y,所以两人跑完一圈花费的时间小陈比小王多6分钟。
87、小张与小王分别从甲、乙两村同时出发,在两村之间往返行走(到达另一村后就马上返回),他们在离甲村3.5千米处第一次相遇,在离乙村2千米处第二次相遇。问他们两人第四次相遇的地点离乙村多远(相遇指迎面相遇)?_____
A: 1千米 B: 1.2千米C: 1.5千米D: 1.8千米
参考答案: A 本题解释:【答案】A。解析:直线多次相遇问题。第二次相遇两人已共同走了甲、乙两村距离的3倍,因此张走了3.5×3=10.5千米。从图上可看出,第二次相遇处离乙村2千米,因此,甲、乙两村距离是10.5-2=8.5千米。每次相遇甲乙二人路程和都比上次相遇多2倍的两地间距。第四次相遇时,两人已共同走了(3+2+2)倍的两村距离,其中张走了3.5×(2×4-1)=24.5千米,24.5=8.5+8.5+7.5千米。因此第四次相遇处,离乙村8.5-7.5=1千米。
88、(2007北京应届,第13题)某车间从3月2日开始每天调入一人,已知每人每天生产1件产品,该车间从3月1日至3月21日共生产840件产品,该车间原有工人多少名?_____
A: 20B: 30C: 35D: 40
参考答案: B 本题解释:参考答案:B题目详解:设车间原有工人n名,则人数应该是一个公差为1的等差数列。根据项数公式: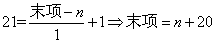 ,根据求和公式:
,根据求和公式: 考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
考查点:数量关系>数学运算>计算问题之算式计算>数列问题>数列求和>单一数列求和>等差数列求和
89、李森在一次村委会选举中,需2/3的选票才能当选,当统计完3/5的选票时,他得到的选票数已达到当选票数的3/4,它还需要得到剩下选票的几分之几才能当选?_____
A: 2500B: 3115C: 2225D: 2550
参考答案: C 本题解释:正确答案是D考点倍数约数问题解析75=3×5×5,共6个约数,质因数每多个3则约数多3个,质因数每多个5则约数多2个,所以A=3×3×3×5×5=675,B=3×5×5×5×5=1875,A+B=2550,故正确答案为D。秒杀技由题意可知,A和B均能被3整除,则其和也能被3整除,仅选项D符合,故正确答案为D。
90、现有50名学生都做物理、化学实验,如果物理实验做正确的有40人,化学实验做正确的有31人,两种实验都做错的有4人,则两种实验都做对的有_____。
A: 27人B: 25人C: 19人D: 10人
参考答案: B 本题解释:参考答案:B题目详解:解法一:A={{物理实验做正确的人}};B={{化学实验做正确的人}}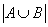 ={{至少做对一种的人数}};
={{至少做对一种的人数}}; ={{两种实验都做对的人}}根据容斥原理可得:
={{两种实验都做对的人}}根据容斥原理可得: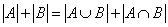 ,代入得:
,代入得: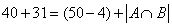 。则
。则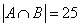 ,所以,选B。解法二:由题意知,两种试验都做错的有4人,则至少做对一种的有46人。而题目已经告知有40人做对物理实验,则说明有6人只做对化学试验。同时有31人作对化学试验,则说明有15人只做对物理实验而做错了化学实验。所以题目的解答为:50-4(全做错)-15(物理对化学错)-6(化学对物理错)=25人。所以,选B。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
,所以,选B。解法二:由题意知,两种试验都做错的有4人,则至少做对一种的有46人。而题目已经告知有40人做对物理实验,则说明有6人只做对化学试验。同时有31人作对化学试验,则说明有15人只做对物理实验而做错了化学实验。所以题目的解答为:50-4(全做错)-15(物理对化学错)-6(化学对物理错)=25人。所以,选B。考查点:数量关系>数学运算>容斥原理问题>两个集合容斥关系
91、参加阅兵式的官兵排成一个方阵,最外层的人数是80人,问这个方阵共有官兵多少人_____
A: 441B: 400C: 361D: 386
参考答案: A 本题解释:正确答案是A考点计算问题解析解析1:设每一排官兵人数为x,x×4-4=80,x=21,则每排官兵人数为21人,那么方阵人数为21×21=441。故正确答案为A。解析2:方正最外层是80人,外层一共4边,但每个顶点上的士兵多计算了一次,得出每一边的人(80+4)÷4=21.方正就是21×21=441。故正确答案为A。
92、有甲、乙两只盒子,甲盒装有2个黑球、4个红球,乙盒装有4个黑球、3个红球,若从甲、乙两盒中各任取两球交换后,甲盒中恰有4个红球的概率为多少?_____
A:  B:
B: 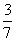 C:
C: 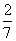 D:
D: 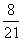
参考答案: D 本题解释:参考答案 题目详解:事件“甲盒中恰有4个红球”发生:说明从甲盒任取两球的结果与从乙盒任取两球的结果相同;甲盒任取两个球:有
题目详解:事件“甲盒中恰有4个红球”发生:说明从甲盒任取两球的结果与从乙盒任取两球的结果相同;甲盒任取两个球:有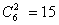 种情形,其中“2黑”的情形有
种情形,其中“2黑”的情形有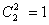 种,“1黑1红”的情形有
种,“1黑1红”的情形有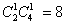 种,“2红”的情形有
种,“2红”的情形有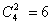 种;乙盒任取两个球:有
种;乙盒任取两个球:有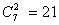 种情形,其中“2黑”的情形有
种情形,其中“2黑”的情形有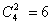 种,“1黑1红”的情形有
种,“1黑1红”的情形有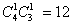 种,“2红”的情形有
种,“2红”的情形有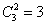 种。所以,“2黑”交换:
种。所以,“2黑”交换: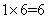 种;“1黑1红”交换:
种;“1黑1红”交换: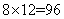 种;“2红”交换:
种;“2红”交换: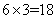 种;因此,甲盒中恰有4个红球的概率是:
种;因此,甲盒中恰有4个红球的概率是: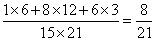 ;所以,选D。考查点:数量关系>数学运算>概率问题>条件概率
;所以,选D。考查点:数量关系>数学运算>概率问题>条件概率
93、(2005上海)棱长为a的正方体 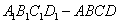 中,求
中,求 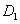 到面
到面 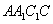 的距离_____。
的距离_____。 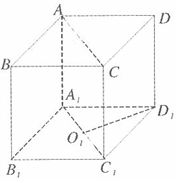
A: 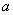 B:
B: 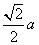 C:
C: 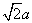 D:
D: 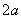
参考答案: B 本题解释:参考答案:B题目详解:根据题意,连接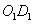 (
( 是
是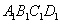 的中心),∵在正方体
的中心),∵在正方体 ,
,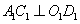 ,
,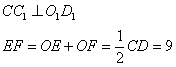 ,且
,且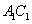 与
与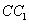 相交与点
相交与点 .∴
.∴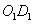
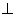 面
面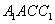 ,∴
,∴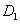 到面
到面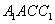 的距离就是求
的距离就是求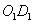 ,则:
,则: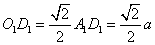 ,所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>与线、角相关问题(立体)
,所以,选B。考查点:数量关系>数学运算>几何问题>立体几何问题>与线、角相关问题(立体)
94、(2006江苏,第9题)算式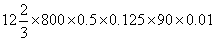 的值是_____。
的值是_____。
A: 312B: 348C: 570D: 286
参考答案: C 本题解释:参考答案:C题目详解:应用因式分解法:原式 。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>因式分解法
。所以,选C。考查点:数量关系>数学运算>计算问题之算式计算>速算与技巧>因式分解法
95、某团体从甲地到乙地,甲、乙两地相距100千米,团体中一部分人乘车先行,余下的人步行,先坐车的人到途中某处下车步行,汽车返回接先步行的那部分人,全部人员同时到达。已知步行速度为8千米/小时,汽车速度为40千米/小时。问使团体全部成员同时到达乙地需要多少时间?_____
A: 5.5小时B: 5小时C: 4.5小时D: 4小时
参考答案: B 本题解释:参考答案:B题目详解:根据题意,二队同时出发又同时到达,则二队步行的距离相等,乘车的距离也相等。设第一队乘车的距离是X,则步行的距离是100-X,那么第二队步行的距离也是100-X,汽车从第一队人下车到回来与第二队相遇所行驶的距离(即空车行使的距离)是:100-2×(100-X)=2X-100根据汽车从出发到与第二队相遇所用时间与第二队步行的时间相同,可列方程:[X+(2x-100)]÷40=(100-x)÷8解得,x=75。所用总时间为(以第一队为例):乘车时间+步行时间=(75÷40)+(100-75)÷8=5小时所以,选B。考查点:数量关系>数学运算>行程问题>相遇问题>直线相遇问题>直线一次相遇问题
96、一个长方体的长、宽、高恰好是三个连续的自然数,并且它的体积数值等于它的所有棱长之和的2倍,那么这个长方体的表面积是_____
A: 74B: 148C: 150D: 154
参考答案: B 本题解释: 【解析】B。设该长方体的长、宽、高分别是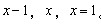 。那么有
。那么有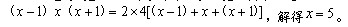 所以这个长方体的表面积为
所以这个长方体的表面积为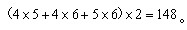
97、某一地区在拆迁时将一些枯死的树木刨出。拆迁办组织三个部门的人员准备将树木锯成短木,树木的粗细都相同,只是长度不一样。甲部门的人锯的树木是2米长,乙部门的人锯的树木是1.5米长。丙部门的人锯的树木是1米长,都要求按0.5米长的规格锯开。时间结束时,三个部门正好把堆放的树木锯完,张三那个部门共锯了27段,李四那个部门共锯了28段,王五那个部门共锯了34段。请问,张三属于哪个部门的?_____
A: 属于丙部门,甲部门最慢B: 属于乙部门,丙部门最慢C: 属于甲部门,丙部门最慢D: 属于乙部门,乙部门最慢
参考答案: B 本题解释:参考答案:B题目详解:张三部门27段=13.5米李四部门28段=14米王五部门34段=17米由于树木都是整根的张三部门一共锯了13.5米所以他们的树木只能是1.5米长的,所以张三是乙部门的。2相对应的王五部门17米长不可能是2米长的只能是1米长的木头,王五是丙部门的。3剩下的李四部门的木头都是2米长的,李四是甲部门的。13.5米=9根木头每根木头锯2次一共是锯了18次;14米=7跟木头每根木头锯3次一共锯了21次;17米=17根木头每根木头锯一次一共锯了17次。所以丙部门最慢。考查点:数量关系>数学运算>计算问题之数的性质>整除问题>整除特征
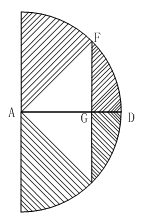
98、如图,AD=DB=DC=10厘米,那么,图中阴影部分的面积是多少平方厘米?_____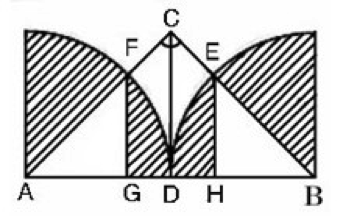
A: 109B: 110C: 107D: 110.25
参考答案: C 本题解释:正确答案是C考点几何问题解析
99、24689-1728-2272的值为_____
A: 689B: 713C: 521D: 479
参考答案: A 本题解释:A【解析】先用心算将两个减数相加,1728+2272=4000。然后再从被减数中减去减数之和,即4689-4000=689。
100、将一个正方形分成9个小正方形,填上1到9这9个自然数,使得任意一个横行,一个纵列以及每一对角线上的3个数之和等于15,请问位于中间的小正方形应填哪个数?_____
A: 4B: 5C: 6D: 7
参考答案: B 本题解释:答案:B【解析】欲保证3个数之和都等于15,只有中间的数字为平均数5才可。